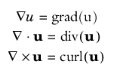The PDE interfaces use a slightly different notation, compared to other physics interfaces and the associated documentation. The difference lies in the definition of the symbol ∇, pronounced
nabla or
del. For the physics interface equation sections and nodes (see
Showing More Options), the
∇ symbol applied to a scalar or vector variable denotes the following coordinate system-independent
gradient,
divergence, and
curl operations:
In the PDE interfaces, nabla/del is interpreted as the vector of partial derivatives:
The spatial coordinates are denoted x1, …,
xn, where
n represents the number of space dimensions. When applied to a scalar or vector in a Cartesian coordinate system, this definition leads to an expression that is identical in form to the gradient, divergence, or curl in the same coordinate system. The same does not apply, however, in curvilinear systems such as the one implied in an axisymmetric geometry.
For example, the divergence of a vector u = [ur, uz] in an axisymmetric cylindrical system is
where β1 , … ,
βn are the components of the vector
β.