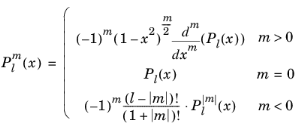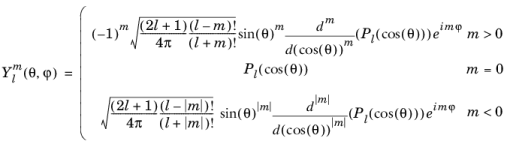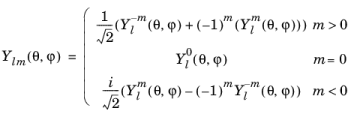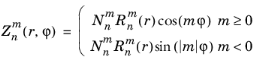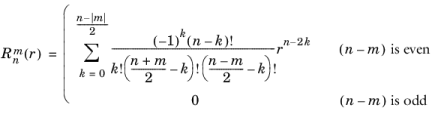Mathematical Functions
The following list includes the built-in mathematical functions that you can use when defining parameters and variables or directly in expressions in the physics interface or feature settings, for example. The function names are reserved names that cannot be used for user-defined functions, but they can be used for variable and parameter names. These functions do not have units for their input or output arguments (unless where noted for trigonometric functions).
Table 5-6: Built-in Mathematical Functions
Name
Description
Syntax
abs
Absolute value
abs(x)
acos
Inverse cosine (in radians)
acos(x)
acosh
Inverse hyperbolic cosine
acosh(x)
acot
Inverse cotangent (in radians)
acot(x)
acoth
Inverse hyperbolic cotangent
acoth(x)
acsc
Inverse cosecant (in radians)
acsc(x)
acsch
Inverse hyperbolic cosecant
acsch(x)
arg
Phase angle (in radians)
arg(z)
asec
Inverse secant (in radians)
asec(x)
asech
Inverse hyperbolic secant
asech(x)
asin
Inverse sine (in radians)
asin(x)
asinh
Inverse hyperbolic sine
asinh(x)
atan
Inverse tangent (in radians)
atan(x)
atan2
Four-quadrant inverse tangent (in radians)
atan2(y,x)
atanh
Inverse hyperbolic tangent
atanh(x)
besselj
Bessel function of the first kind
besselj(n,z)
bessely
Bessel function of the second kind
bessely(n,z)
besseli
Modified Bessel function of the first kind
besseli(n,z)
besselk
Modified Bessel function of the second kind
besselk(n,z)
binomial
Binomial coefficient
binomial(n,k)
ceil
Nearest following integer
ceil(x)
conj
Complex conjugate
conj(x)
cos
Cosine
cos(z)
cosh
Hyperbolic cosine
cosh(x)
cot
Cotangent
cot(x)
coth
Hyperbolic cotangent
coth(x)
csc
Cosecant
csc(z)
csch
Hyperbolic cosecant
csch(x)
erf
Error function
erf(x)
erfinv
Inverse error function
erfinv(x)
exp
Exponential function ex. That is, exp(1) is the mathematical constant e (Euler’s number)
exp(x)
factorial
Factorial of nonnegative integer
factorial(n)
floor
Nearest previous integer
floor(x)
gamma
Gamma function
gamma(x)
imag
Imaginary part
imag(x)
legendre
Legendre polynomial and associated Legendre polynomial of integer degree and order (see legendre for more information)
legendre(l,x)
legendre(l,m,x)
log
Natural logarithm
log(x)
log10
Base-10 logarithm
log10(x)
log2
Base-2 logarithm
log2(x)
max
Maximum of two arguments
max(x,y)
min
Minimum of two arguments
min(x,y)
mod
Modulo operator
mod(x,y)
psi
Psi function and its derivatives (psi(0,x) is the digamma function)
psi(k,x)
random
Random function, uniform distribution
random(x,y,…)
randomnormal
Random function, normal (Gaussian) distribution
randomnormal(x,y,…)
range
Create a range of numbers (see Entering Ranges and Vector-Valued Expressions)
range(start,step,end)
real
Real part
real(x)
round
Round to closest integer or to closest number with specified precision p (number of decimal digits). For negative p, round to closest integer number divisible by 10^(-p).
round(x)
round(x,p)
sec
Secant
sec(z)
sech
Hyperbolic secant
sech(x)
sign
Signum function
sign(x)
sin
Sine
sin(z)
sinh
Hyperbolic sine
sinh(x)
sphericaly
Spherical harmonic function (see sphericaly for more information)
sphericaly(l,m,theta,phi)
sphericalyr
Real spherical harmonic function (see sphericalyr for more information)
sphericalyr(l,m,theta,phi)
sqrt
Square root
sqrt(x)
tan
Tangent
tan(z)
tanh
Hyperbolic tangent
tanh(x)
zernike
Zernike polynomial function (see zernike for more information
zernike(n,m,r,phi)
legendre
The legendre(l,x) function evaluates a Legendre polynomial Pl(x) of integer degree l:
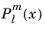
The legendre(l,m,x) function evaluates an associated Legendre polynomial of integer degree l and order m:
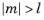
The degree l must be a nonnegative constant integer, and the order m must be a constant integer. For , legendre(l,m,x) returns zero.
sphericaly
The sphericaly(l,m,theta,phi) function evaluates the spherical harmonic function :
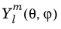
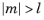
where Pl is the Legendre polynomial of degree l. The degree l must be a nonnegative constant integer, and the order m must be a constant integer. For , sphericaly(l,m,theta,phi) returns zero.
sphericalyr
The sphericalyr(l,m,theta,phi) function evaluates the real spherical harmonic function :
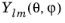
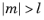
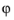
The degree l must be a nonnegative constant integer, and the order m must be a constant integer. For , sphericalyr(l,m,theta,phi) returns zero. The arguments θ and must be real.
zernike
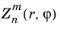
The zernike(m,n,r,phi) function evaluates a Zernike polynomial defined in the following way:
where is the radial part:
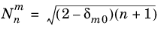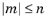
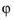
and is the normalization factor. The n argument is required to be a nonnegative constant integer, and the m argument is required to be a constant integer satisfying . The r and arguments are required to be real.