model.component(<ctag>).coordSystem().create(<tag>,<gtag>,type) creates a coordinate system with tag <tag> on geometry <gtag> of type type. There are the following types of coordinate systems: mapped system (Mapping), base-vector system (VectorBase), rotated system (Rotated), boundary system (Boundary), scaling system (Scaling), cylindrical system (Cylindrical), and system from geometry (SystemFromGeometry). The boundary system only applies to boundaries. In addition, the perfectly matched layers (PMLs), infinite elements, and absorbing layers are also implemented as types of coordinate systems: PML, InfiniteElement, and AbsorbingLayer, respectively.

model.component(<ctag>).coordSystem(<tag>).selection().named(<seltag>) assigns the coordinate system to the named selection <seltag>. model.component(<ctag>).coordSystem(<tag>).selection().set(...) defines a local selection that assigns the coordinate system to geometric entities. For a complete list of methods available under selection(), see Selections. The selection method is only available for coordinate systems of the following types: Scaling, PML, InfiniteElement, and AbsorbingLayer.

model.component(<ctag>).coordSystem(<tag>).set("orthonormal","on") specifies that this is a orthonormal system. This affects the internal calculation of systems, so some simplifications on expressions can be made. It is recommended to use this option when possible. Boundary systems, rotated systems, and cylindrical system are always orthonormal..

model.component(<ctag>).coordSystem().create(<tag1>,<gtag>,"Mapping") creates a mapped system. In a mapped system you specify the coordinate mapping given in some of the available frame coordinates (usually x, y, z).

model.component(<ctag>).coordSystem(<tag1>).setIndex("map", "x+1", 0) sets the mapping of the first coordinate system coordinate to be a function of the first frame coordinate, x.

model.component(<ctag>).coordSystem(<tag1>).setIndex("map", "y+1", 2) sets the mapping of the third coordinate system coordinate to be a function of the second frame coordinate y.

model.component(<ctag>).coordSystem().create(<tag2>,"VectorBase") creates a base-vector system. In a base-vector system you specify the base vectors given as components of a frame system. If the components are independent of frame coordinates this is a linear system and can be applied for any frame.

model.component(<ctag>).coordSystem(<tag2>).setIndex("base", "1", 0, 1) sets the first base vector’s second component to one. As an alternative, it is possible to specify the full base-vector matrix using the following syntax:

model.component(<ctag>).coordSystem(<tag2>).set("base",
new String[][]{{"0","1","0"},{"0","0","1"},{"1","0","0"}}) sets the base vector matrix so the first base vector is equal to the y-axis of the frame system, the second is the z-axis, and so on. In 2D, you only use a two rows and two columns from the full base vector matrix for the in-plane base vectors. As an option, it is therefore possible to specify which of the coordinate system base vectors that corresponds to the out-of-plane axis in the frame system. Internally, this base vector always gets the components {"0","0","1"}. The third column is also set using these components. To make a general 3D system in 2D, you must use the mapped system.

model.component(<ctag>).coordSystem(<tag2>).set("outofplane", "2") sets the third base vector to represent the out-of-plane vector (z-axis in 2D). The value is zero based. In 1D the out-of-plane index is set using the syntax “1,2” to set second and third base vectors to represent the out-of-plane vector.

model.component(<ctag>).coordSystem().create(<tag3>,"Rotated") creates a rotated system. In 3D you specify the Z-X-Z Euler angles, which corresponds to sequential rotation first about the z-axis, then the x-axis, and finally the z-axis again. In 2D you can either specify a full 3D rotation or a rotation only about a selected out-of-plane axis.

model.component(<ctag>).coordSystem(<tag3>).setIndex("angle","12[deg]",0) sets the first rotation about the z-axis to 12 degrees. The default unit for angles are radians.

model.component(<ctag>).coordSystem().create(<tag4>,<gtag>,"Boundary") creates a new boundary system, which is a local base vector system on 2D boundaries (t, n) and on 3D boundaries (t1, t2, n). There is always one boundary system added by default for each geometry.

model.component(<ctag>).coordSystem(<tag4>).set("reversenormal","on") flips the normal direction for this system, so that it is opposite to the normal direction given by the geometry.

model.component(<ctag>).coordSystem(<tag4>).set("mastersystcomp","2") sets the first tangential direction from the second axis of the specified master system.

model.component(<ctag>).coordSystem(<tag4>).set("mastersystem","manual") specifies that no master system is used and that the tangential direction must be entered by the user.

model.component(<ctag>).coordSystem(<tag4>).setIndex("tangent","1") sets the first component of the first tangential direction.

In addition, you can add ReverseNormal and DomainNormal subfeatures to reverse the normal for some boundaries and switch the normal direction on the exterior of some domains, respectively.

model.component(<ctag>).coordSystem(<tag4>).create(<rntag>, "ReverseNormal") creates a ReverseNormal subfeature. To it, you then assign a boundary selection. For boundary 3, for example, use model.component(<ctag>).coordSystem(<tag4>).feature(<rntag>).selection().set(3);

model.component(<ctag>).coordSystem(<tag4>).create(<dntag>, DomainNormal") creates a DomainNormal subfeature. To it, you then assign a domain selection. For domain 2, for example, use model.component(<ctag>).coordSystem(<tag4>).feature(<dntag>).selection().set(3);. There is one property for the DomainNormal subfeature: normalDirection, which can be a string outward (the default) or inward.

model.component(<ctag>).coordSystem().create(<tag5>,<gtag>,"Cylindrical") creates a cylindrical coordinate system, which you can use in 2D and 3D where rotational symmetry about the axis is required. You can specify the origin, axis direction and radial base vector.

model.component(<ctag>).coordSystem(<tag5>).set("origin", new String[]{"1","0","0"}) sets the origin to (1,0,0).

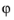
model.component(<ctag>).coordSystem().create(<tag6>,<gtag>,"Spherical") creates a spherical coordinate system, which you can use in 3D to define a field or property using spherical coordinates. You can specify the origin, zenith axis (θ = 0), and azimuth axis (θ = π/2, = 0).

model.component(<ctag>).coordSystem(<tag6>).set("origin", new String[]{"1","0","0"}) sets the origin to (1,0,0).

model.component(<ctag>).coordSystem().create(<tag7>,<gtag>,"FromGeometry") creates a coordinate system taken from a work plane in a 3D geometry or defined in a 3D geometry part that is included in the geometry as a part instance. You can specify which work plane to use:.

model.component(<ctag>).coordSystem().create(<tag8>,<gtag>,"Scaling") creates a scaling coordinate system that maps the geometry, as represented by the independent coordinates of an underlying frame, onto a virtual geometry represented by virtual scaling system coordinates. Physics interfaces that support infinite elements or perfectly matched layers accept the scaling system coordinates as being the physical domain, in which the underlying frame coordinates are seen as a parameterization. Therefore, using a scaling coordinate system you can arbitrarily deform the domain.

model.component(<ctag>).coordSystem(<tag8>).setIndex("map", "y+1", 1) sets the second coordinate mapping to y+1.

model.component(<ctag>).coordSystem().create(<tag9>,<gtag>,"Combined") creates a combined coordinate system that makes it possible to use different coordinate systems in different domains, for example. To add a coordinate system to the combined system and define it on domain 2, use

model.component(<ctag>).coordSystem().create(<tag9>,<gtag>,"Composite") creates a composite coordinate system that defines a new coordinate system by multiplying the transformation matrices of two other coordinate systems.

model.component(<ctag>).coordSystem().create(<tag10>,<gtag>,"PML") creates a PML (perfectly matched layer), which acts as an artificial absorbing layer in a domain for a wave simulation. You can specify the type and scaling of the PML using the following properties:

model.component(<ctag>).coordSystem().create(<tag11>,<gtag>,"InfiniteElement") creates an infinite element, which acts as an unbounded domain for a simulation. You can specify the type and scaling of the infinite element using the following properties:

model.component(<ctag>).coordSystem().create(<tag12>,<gtag>,"AbsorbingLayer") creates an absorbing layer, which acts as an effective nonreflecting-like boundary condition in transient simulations using a time-explicit solver. You can specify the type and scaling of the absorbing layer using the following properties:

Create a cylindrical coordinate system with a radial base vector direction that is (0, 1, 0); that is, a coordinate that points in the global y direction: