Theory for the Reactive Pellet Bed

The Reactive Pellet Bed, available to users of the Chemical Reaction Engineering Module, adds to the Transport of Diluted Species interface a domain feature that can simulate regions filled with reactive catalyst pellets, as in packed bed reactors. The pellets are simulated with the Extra Dimension technology provided by the COMSOL software: A 1D, 2D, or 3D domain represents the bed volume. The extra dimension is the added radial microscale dimension inside each pellet.


	For an example of how to use the Reactive Pellet Bed, see the model example A Multiscale 3D Packed Bed Reactor, file path Chemical_Reaction_Engineering_Module/Reactors_with_Porous_Catalysts/packed_bed_reactor_3d

Figure 3-3: Schematic showing the macroscale (bed volume) and the microscale (pellet).

The transport and reaction equations inside the pellets are solved on an extra dimension attached to the 1D, 2D, or 3D physics interfaces, including axisymmetric cases.

The equations inside the spherical pellet are solved as a spherical transport equations on a nondimensional radial coordinate on the domain 0-1. A given pellet size or a discrete distribution of sizes can be used.

The model equations assume spherical particles (pellets) of a radius rpe. Modeling assumptions for cylinders, flakes, and user-defined shapes can also be used. Consider the microscale concentration cpe inside an individual porous pellet or pellets, and the macro-concentration c in the packed bed gas volume.

The pellet radius input can be:

•

One uniform pellet radius, which can be space dependent f (x, y, z).

•

Binary, ternary, and so on, mix up to 5 radii. The user inputs a table with the mix of sizes (1 mm, 2 mm, for example), and a volume fraction of each. Different chemical reactions per pellet size can be specified.

The model equation for the bulk (macroscale) species is, for example:

(3-21)

•

εb is the bed porosity.

•

The dependent variable c for each chemical species i represents the interstitial concentration, that is, the physical concentration based on unit volume of fluid flowing between the pellets.

•

Ri is the species reaction rate in the bed. This corresponds to reactions occurring in the pore space outside of the pellets. Note, that Ri is the reaction rate per unit volume of bed.

Looking inside a pellet: Assuming no concentration variations in the space-angle (θ,

) direction, but only in the radial (r) direction of the spherical pellet allows a spherically symmetric reaction-diffusion transport equation inside the pellet. If rdim (SI unit: m) is the spatial radial coordinate in the pellet, and rpe is the pellet radius, the nondimensional coordinate r = rdim/rpe can be defined. The modeling domain on r goes from 0 to 1.

Figure 3-4: Modeling domain in a pellet for dimensional (top) and nondimensional (bottom) coordinates.

A shell mole balance across a spherical shell at radius rdim (SI unit: m), and a subsequent variable substitution r = rdim/rpe gives the following transport equation on the pellet domain 0 < r < 1:

(3-22)

•

εpe is the pellet (microscale) porosity.

•

As in Equation 3-22, cpe is the interstitial (physical) species concentration in moles/m3 of fluid volume element inside the pore channel.

•

Rpe,i is the pellet reaction rate. This corresponds to reactions taking place inside the pellets. Note that the user input of Rpe, iis per unit volume of pellet.

Assuming that the pellets bed is homogenized, that is that pellets are present in an averaged sense in each point of the geometry, the equation to be solved in the reactive bed is:

(3-23)

where N is the number of pellets per unit volume of bed:

Dividing Equation 3-22 with the pellet by

(the pellet area times r2), the governing equation inside the each pellet is:

(3-24)

The effective diffusion coefficient in the equations above depends on the porosity εpe, tortuosity τ, and physical gas diffusivity D in the manner of

The available models for the porous media tortuosity are the one by Millington and Quirk (Ref. 12),

(3-25)

the Bruggeman model,

(3-26)

and the Tortuosity model, where the tortuosity expression is entered as user defined input.

These are readily used for both gaseous and liquid fluids along with various types of pellet shapes. For instance, the first model has been shown to fit mass transport in soil-vapor and soil-moisture well.

Equation 3-22 can be solved for two types of boundary conditions at the interface between the pellet surface and the fluid in this feature.

•

assuming that all resistance to mass transfer to/from the pellet is within the pellet and no resistance to pellet-fluid mass transfer is on the bulk fluid side. The concentration in the fluid will thus be equal to that in the pellet pore just at the pellet surface:

. This constraint also automatically ensures flux continuity between the internal pellet domain and the free fluid domain through so-called reaction forces in the finite element formulation.

•

The flux of mass across the pellet-fluid interface into the pellet is possibly rate determined on the bulk fluid side by film resistance. The resistance is expressed in terms of a film mass transfer coefficient, hDi, such that:

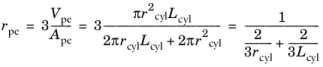(3-27)

where Ni, inward is the molar flux from the free fluid into a pellet and has the unit moles/(m2·s).

With the film resistance formulation above, the free fluid Equation 3-21 needs to be amended for flux continuity so that

(3-28)

where Sb (SI unit: m2/m3) is the specific surface area exposed to the free fluid of the packed bed (not including the inside of the pores).

For the case of randomly packed spherical pellets, the specific surface area exposed to the free fluid is (Ref. 3):

(3-29)

The mass transfer coefficient in Equation 3-27 can be computed from the fluid properties and flow characteristics within the porous media. For this, the Sherwood, Sh, number defined as the ratio between the convective mass transfer coefficient and the diffusive mass transfer coefficient is often used:

where L is a characteristic length (for spheres, typically the radius), and D is the diffusion coefficient in the fluid. From the Sherwood number definition, the mass transfer coefficient can be computed.

Three commonly used empirical expressions for the calculation of the Sherwood number are the Frössling relation (Ref. 4):

(3-30)

which was measured on pellets in the size region 1 mm, the Rosner relation (Ref. 5)

(3-31)

and the Garner and Keey relation (Ref. 4)

(3-32)

which was measured for Re numbers greater than 250.

All three depend on the Reynolds, Re, and Schmidt, Sc, numbers. The first describing the fluid flow regime (laminar versus turbulent) and the second, the ratio between the viscous diffusion rate and the molecular (mass) diffusion rate. In the expressions, properties such as velocity, u, dynamic viscosity, μ, and density, ρ, of the fluid are included.

Surface Species

Surface species correspond to species bound to the solid interface within the porous pellet, which is also in contact with the pore fluid. The surface species hence only exists within the pellet. The surface species are assumed to be immobile, and the concentration is only dependent on the reaction rate of surface reactions involving the species:

(3-33)

It can be noted that there is no mass flux of surface species within the pellet or across the pellet outer surface and the bulk fluid. The unit of surface species concentration cpes is amount per area, and the corresponding surface reaction rate unit is amount per area and time.

When surface species are present, the equation governing transport of bulk species inside the each pellet is:

(3-34)

The second term on the right hand side represents species production or removal due to surface reactions in the pellet. It is composed of the reactive specific area Sb,reac, the area per volume available for surface reactions, and the surface reaction rate

It should be noted that the surface reaction rate for a bulk species

and the surface reaction rate for a surface species

Nonspherical Particles

For nonspherical pellets (of any shape), the relations above can be applied approximately by reinterpreting the pellet radius rpe as

(3-35)

(Ref. 14), where Vpe and Ape are the volume and external surface, respectively, of a single pellet of any shape. Since the specific surface Spe (SI unit: m2/m3) of one pellet is defined as

it follows by insertion of Equation 3-35 that

For a packed bed of which the packing has a porosity εb, the specific surface of the bed will be

(3-36)

for any pellet shape. Now rpe and Sb can be calculated for any shape and inserted in equations Equation 3-22 and Equation 3-28. Some common specific shapes have automatic support:

Cylinders

For cylindrical shapes, applying Equation 3-35 gives

(3-37)

It is common practice to assume that the top and bottom surface of cylindrical pellets have negligible effect on the mass transfer to and from the internals of the pellet, or,

. Equation 3-37 then simplifies to

and Equation 3-36 to

Flakes

The derivation for a disc-shaped catalyst pellet is exactly the same as for cylindrical pellets, except that the assumption is reversed about the end surfaces and the envelope surface:

, where wflake is the thickness of the disc. This gives

and

Surface Reaction

Surface reactions can also be simulated inside the pellet. Surface species are introduced into pellet by adding them in the Surface Species section of the Reactive Pellet Bed feature.

A bulk species can take part in both volumetric and surface reactions. The total reaction rate for a bulk species within a pellet is defined as:

Here Rpe is the reaction rate for bulk reactions occurring inside the pellet. Rpe,s and Sb are the reaction rate and the reactive specific surface area for a surface reaction occurring inside the pellet, on the interface between the solid matrix and the fluid.

Heat Source

The heat source of endothermic or exothermic reactions inside the pellet needs to be accounted for in the heat transfer on the bulk level if the heat balance is not solved within the pellet. Thermal equilibrium is assumed in each pellet, and the source is averaged across the pellet:

(W/m3)

If there are multiple pellet sizes i in the bed the heat source computed by summing over all sizes:

Here θv,i is the volume fraction of pellet i in the pellet mix.