The Laminar Flow interfaces provide various predefined inelastic non-Newtonian constitutive models including Power law, Carreau, Bingham–Papanastasiou, Herschel–Bukley–Papanastasiou and Casson–Papanastasiou.

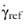
where m, n are scalars that can be set to arbitrary values and denotes a reference shear rate for which the default value is 1 s−1. For n > 1, the power law describes a shear thickening (dilatant) fluid. For n < 1, it describes a shear thinning (pseudoplastic) fluid. A value of n equal to one gives the expression for a Newtonian fluid.

Equation 3-18 predicts an infinite viscosity at zero shear rate for n < 1. This is however never the case physically. Instead, most fluids have a constant viscosity for shear rates smaller than 10−2 s−1 (Ref. 21). Since infinite viscosity also makes models using Equation 3-18 difficult to solve, COMSOL Multiphysics implements the Power law model as

where is a lower limit for the evaluation of the shear rate magnitude. The default value for is 10−2 s−1, but can be given an arbitrary value or expression using the corresponding text field.

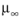
where λ is a parameter with the unit of time, μ0 is the zero shear rate viscosity, is the infinite shear-rate viscosity, and n is a dimensionless parameter. This expression is able to describe the viscosity for most stationary polymer flows.

Viscoplastic fluid behavior is characterized by existence of the yield stress τy — a limit which must be exceeded before significant deformation can occur. To model the stress-deformation behavior of viscoplastic materials, different constitutive equations have been propose. The Bingham plastic model is written as

where μp is the plastic viscosity.

To allow computation in both yielded and unyielded region, the Papanastasiou continuous regularization for the viscosity function is used:

where mp is a scale that controls the exponential growth of stress.

The Herschel-Bulkley -Papanastasiou model combines the effects of the Power law the Papanastasiou continuous regularization:

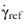
where m, n are scalars that can be set to arbitrary values, and is the reference shear rate. In case n equals one, the Bingham-Papanastasiou model is recovered. This equation is valid in both yielded and unyielded regions. The exponent mp controls the smoothness of the viscosity function.