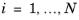
The model equations that are solved in the Phase Transport Mixture Model interfaces are based on the mass conservation of each phase and on conservation of momentum. The mass conservation equation for each (immiscible) phase is given by:

where ρi denotes the density (SI unit: kg/m3), si denotes the volume fraction (dimensionless), and ui denotes the velocity vector (SI unit: m/s) of phase i. In addition, the term Qi denotes a mass source for phase i (SI unit: kg/(m3·s)). It is assumed that the sum of the volume fractions of the phases equals 1:

This means that N − 1 phase volume fractions are independent and are possible to solve for using Equation 6-112. The volume constraint Equation 6-113 is used to reduce the number of dependent variables: one volume fraction, let us say of phase ic (to be specified in the main node of the coupled Phase Transport interface), is expressed using the other volume fractions:

In the Mixture Model multiphysics coupling feature, it is assumed that the phase ic is the continuous phase.

Furthermore, the mass averaged mixture velocity j is defined as:

Here ρ is the mixture density (SI unit: kg/m3) given by:

The relative velocity uri of phase i is defined as:

This relative velocity uri is assumed to be given by two terms

where the slip velocity uslip,i (SI unit: m/s) in the first term is given by one of the slip velocity models discussed below, and where the second term accounts for the turbulent effects, with Dmd (SI unit: m2/s) a turbulent dispersion coefficient given by

where σT is the turbulent particle Schmidt number (dimensionless). The particle Schmidt number is usually suggested a value ranging from 0.35 to 0.7.

With the previous definitions, the mixture velocity j can be rewritten as

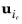
From this equation, and using the volume constraint Equation 6-113, the velocity of the continuous phase can be written in terms of the mixture velocity j and the slip velocities uslip,i as follows:

Here the velocity field ur is the mass average of all relative velocities:

and τGm is the sum of the viscous and turbulent stresses (SI unit: kg/(m·s2)). The last term between parenthesis on the first line of Equation 6-123 is called the diffusion stress.