Moist air is generated from Thermodynamics in the Pressure Reciprocity Calibration Coupler with Detailed Moist Air Material Properties tutorial. Application Library path
Acoustics_Module/Tutorials,_Thermoviscous_Acoustics/pressure_reciprocity_calibration_coupler
Acoustics_Module/Tutorials,_Thermoviscous_Acoustics/pressure_reciprocity_calibration_coupler
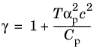 .
.