Pressure Acoustics, Time Explicit Model

The node adds the equations to model the transient propagation of linear acoustics waves based on the dG-FEM time explicit method. For the time explicit method used, the governing equations are formulated as a first order system, in terms of the linearized continuity equation and the linearized momentum equation, as

where t is time, pt is the total acoustic pressure, ut is the total acoustic velocity, ρ is the fluid density, c is the speed of sound, and I is the unit matrix. Domain sources like a Mass Source, Heat Source, or Volume Force Source can be defined through the right hand sides Qm and qd. These two source terms represent the same quantities as the Monopole Domain Source and the Dipole Domain Source in The Pressure Acoustics, Frequency Domain Interface and The Pressure Acoustics, Transient Interface.

The dependent variables are the acoustic pressure p and the acoustic velocity u (sometimes called particle velocity or perturbation velocity). The equations are formulated in the total fields pt and ut which is the sum of the scattered field (the dependent variable solved for) and a possible background field pb and ub. The background field can be set up using the Background Acoustic Field feature.

The equations solved are the linearized Euler equations in a quiescent setting. The equations are easily combined to generate the scalar wave equation solved in The Pressure Acoustics, Transient Interface as discussed in Theory Background for the Pressure Acoustics Branch.

In the formulation of the wave equation, the speed of sound c and density ρ may in general be space dependent but only slowly varying in time, that is, at a time scale much slower than the variations in the acoustic signal.

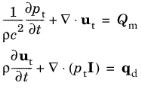
	The equations solved in the Pressure Acoustics, Time Explicit interface are closely related to the equations solved in The Convected Wave Equation, Time Explicit Interface. There is no background flow option in the Pressure Acoustics, Time Explicit interface but, on the other hand, it uses a scattered field formulation that allows solving scattering problems. For nonlinear acoustic problems The Nonlinear Pressure Acoustics, Time Explicit Interface should be used.

In the window, define the properties for the acoustics model and model inputs including temperature.

Select a : (the default), , , , , or .

•

If , , or is selected enter the fluid properties (see the Transient Pressure Acoustics Model for details). These three options will define the sound diffusivity δ through the classical material properties. The options are equivalent to defining the classical thermoviscous attenuation factor atv in the frequency domain.

•

If is selected enter the speed of sound c, the density ρ, and the sound diffusivity δ. This option can be used for modeling fluids with measured damping properties. The relation between the sound diffusivity δ and the equivalent (plane wave) attenuation coefficient α, at a given frequency f, is given by the expression

For all options, the default is to use the material property values from , select from the list to enter a user-defined value or expression in the text field that appears. For numerical stability reasons it is recommended to use physical values of attenuation properties.

Selecting any of the dissipations models will modify the governing Equation 2-2 by adding a right hand side to the momentum equation defined as

This term has a small cost on the computation time when solving the model. The term has to be evaluated at every time-step taken by the solver.

To display this section, click the button (

) and select in the dialog box. In this section, you specify the value of the Lax-Friedrichs flux parameter τLF (default value: 0.2). This value controls the numerical flux between the elements (nodal discontinuous Lagrange elements) used with the discontinuous Galerkin (DG) method. The numerical flux defines how adjacent elements are connected and how continuous p and u are. Different definitions of the numerical flux lead to different variants of the DG method. The flux implemented here is the so-called global Lax-Friedrichs numerical flux. The value of the parameter τLF should be between 0 and 0.5. For τLF = 0 a so-called central flux is obtained. Setting τLF = 0.5 gives a maximally dissipative global Lax-Friedrichs flux.

	For general information about the numerical flux see the Numerical Flux section under Wave Form PDE in the COMSOL Multiphysics Reference Manual.

To display this section, click the button (

) and select in the dialog box. By default, the filter parameters α, ηc, and s are not active. Select the check box to activate the filter. The filter provides higher-order smoothing for the DG formulation. Inside absorbing layers the settings given here are overridden by the Filter Parameters for Absorbing Layers.