It is possible to compute the ray intensity by changing Intensity computation to
Compute intensity or
Compute intensity in graded media in the Settings window for the Ray Acoustics interface. The options
Compute intensity and power and
Compute intensity and power in graded media can also be used to compute intensity, with the only difference being that these options define an additional auxiliary dependent variable for the total power transferred by the ray. The setting
Compute intensity is more robust and accurate than
Compute intensity in graded media, but is only applicable to homogeneous media. The setting
Compute intensity in graded media can be used for both homogeneous and graded media, but it introduces more numerical error than
Compute intensity.
When Compute intensity is selected, the ray intensity is computed along each ray path using the following assumptions:
The calculation of ray intensity in graded media is based on the concept of a curvature tensor K, defined in terms of the principal curvatures
κ1 and
κ2 and the corresponding principal curvature directions
e1 and
e2:
Because e1 and
e2 are orthogonal, it follows that
κ1 and
κ2 are eigenvalues of
K. It also follows that
K is singular because there is no contribution that is orthogonal to both
e1 and
e2.
The selection of the coordinate system in which the curvature tensor is defined is crucial. It is convenient to describe the coordinate system so that two of the coordinate axes lie in the plane containing e1 and
e2, since this reduces the number of nonzero terms in
K. Further reduction in the number of nonzero terms can be achieved if
K can be defined in a coordinate system in which
e1 and
e2 are basis vectors. This is possible in 2D because one of the principal curvature directions is always parallel to the out-of-plane direction, but in 3D it is not feasible because the principal curvature directions can change as rays propagate through a graded medium.
In 2D, one of the principal curvature directions is always known, so it is possible to define s1 and
s2 so that they coincide with
e1 and
e2. The rotation matrix
Q0 is the identity, and the auxiliary dependent variable for the angle
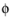
can be omitted.
Following Ref. 3, the derivative of the curvature tensor along the ray trajectory in a graded medium is given by the expression
where the terms Mi correspond to the different ways in which the curvature can depend on the medium properties. They are defined using the following expressions:
where Π is the projection matrix:
The gradient operator ∇S consists of derivatives that are taken with respect to the local coordinates with basis vectors
s1,
s2, and
t.
By application of the chain rule, the derivatives of the nonzero elements of KS can be expressed in terms of the principal curvatures that occupy the diagonal elements of
KW and the rotation angle
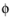
:
The principal curvatures κ1 and
κ2 are not ideal choices for the auxiliary dependent variables stored by each ray because their values can become arbitrarily large as rays approach caustics. Similarly, the principal radii of curvature
r1 and
r2 are not ideal choices because their values can become arbitrarily large when a diverging wavefront begins to converge while propagating through a graded medium.
Instead, the auxiliary dependent variables stored by each ray are the help variables α1 and
α2. In 2D, only one help variable is allocated because the out-of-plane principal radius of curvature is assumed to be infinite. The principal curvatures are expressed in terms of the help variables using the expression
where κ0 =
1 1/m and
i ∈ [1, 2]. The derivatives are then related by the expression
where I0 =
1 W/m
2. The relationship between the ray intensity help variable and the principal curvatures is
where α is the attenuation coefficient of the medium.