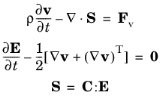Elastic Waves, Time Explicit Model

The node adds the equations for modeling the propagation of linear elastic waves. Define the properties of a general isotropic or anisotropic material. The model solves the governing equations for a general liner elastic material in a velocity-strain formulation

where v is the velocity, ρ the density, S the stress tensor, E the strain tensor, C is the elasticity tensor (or stiffness tensor), and Fv is a possible body force. The equations are valid for both isotropic and anisotropic material data. Bulk dissipation can be added by using the Damping subnode.

The is selected by default. The list contains all applicable coordinate systems in the component. The coordinate system is used for interpreting directions of orthotropic and anisotropic material data and when stresses or strains are presented in a local system.

	Coordinate systems with directions which change with time should not be used.

Define the representation of the material. Choose:

•

for a linear elastic material that has different material properties in orthogonal directions, so that its stiffness depends on the properties Ei, νij, and Gij.

•

for a linear elastic material that has different material properties in different directions, and the stiffness comes from the symmetric elasticity matrix, D

If orthotropic or anisotropic is selected then also select the to (the default) or notation. This option defines what numbering and notation is used for entering user defined material data and when defining material properties in the node.

For an , from the list select a pair of elastic properties for an isotropic material — , , , , or . For each pair of properties, select from the applicable list to use the value or enter a value or expression.

Each of these pairs define the elastic properties and it is possible to convert from one set of properties to another according to Table 3-1.

Table 3-1: Expressions for the elastic moduli.
Description	Variable	D(E,ν)	D(E,G)	D(K,G)	D(λ,μ)
Young’s modulus	E =	E	E
Poisson’s ratio	ν =	ν
Bulk modulus	K =			K
Shear modulus	G =		G	G	μ
Lamé parameter λ	λ =				λ
Lamé parameter μ	μ =		G	G	μ
Pressure- wave speed	cp =
Shear-wave speed	cs =

The individual property parameters are:

•

(transverse wave speed) cs. This is the wave speed for a solid continuum. In plane stress, for example, the actual speed with which a longitudinal wave travels is lower than the value given.

When is selected from the list, the material properties vary in orthogonal directions only. The can be specified in either or notation. When is selected in 3D, enter three values in the fields for E, ν, and the G. This defines the relationship between engineering shear strain and shear stress. It is applicable only to an orthotropic material and follows the equation

	νij is defined differently depending on the application field. It is easy to transform among definitions, but check which one the material uses.

When is selected from the list, the material properties vary in all directions, and the stiffness comes from the symmetric , D. The can be specified in either or notation. When is selected, a 6-by-6 symmetric matrix is displayed.

	Note that the 6-by-6 Elasticity matrix, D has to be complete regardless of the spatial dimension of the problem. This is due to the generalized plane strain formulation of the governing equations solved in 2D.

The default ρ uses values . For enter another value or expression. If any material in the model has a temperature dependent mass density, and is selected, the list will appear in the section. As a default, the value of Tref is obtained from a . You can also select to enter a value or expression for the reference temperature locally.

To display this section, click the button (

) and select in the dialog box. In this section, you specify the value of the Lax–Friedrichs flux parameter τLF (default value: 0.2). This value controls the numerical flux between the elements (nodal discontinuous Lagrange elements) used with the discontinuous Galerkin (dG) method. The numerical flux defines how adjacent elements are connected and how continuous v and E are. Different definitions of the numerical flux lead to different variants of the dG method. The flux implemented here is the so-called global Lax–Friedrichs numerical flux. The value of the parameter τLF should be between 0 and 0.5. For τLF = 0 a so-called central flux is obtained. Setting τLF = 0.5 gives a maximally dissipative global Lax–Friedrichs flux.

	For general information about the numerical flux see the Numerical Flux section under Wave Form PDE in the COMSOL Multiphysics Reference Manual.

To display this section, click the button (

) and select in the dialog box. By default, the filter parameters α, ηc, and s are not active. Select the check box to activate the filter. The filter provides higher-order smoothing for the dG formulation and can be used to stabilize the solution. Inside absorbing layers the settings given here are overridden by the Filter Parameters for Absorbing Layers.

Enter values for the filter parameters in the corresponding text fields (default values: 36, 0.6, and 3). α must be positive and lie between 0 and 36. α = 0 means no dissipation and α = 36 means maximal dissipation. ηc should be between 0 and 1, where 0 means maximal filtering and 1 means no filtering (even if filtering is active). The s parameter should be larger than 0 and controls the order of the filtering (a dissipation operator of order 2s). For s = 1, you get a filter that is related to the classical 2nd-order Laplacian. A larger s gives a more pronounced low-pass filter.

	For more detailed information about the filter see the Filter Parameters section under Wave Form PDE in the COMSOL Multiphysics Reference Manual.

To display this section, click the button (

) and select in the dialog box. The maximum wave speed enters the expression for the cell wave time scale used by the solver to estimate a stable internal time step. Select (the default) or . With the option the maximum speed is set equal to the pressure wave speed, for enter another value for cmax. The estimate for isotropic materials is correct, but for certain configurations of anisotropic materials it can be necessary to enter a larger value to ensue numerical stability.