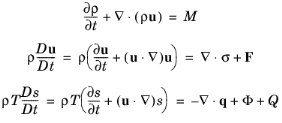The equations governing the physics in any fluid are the foundation for deriving the linearized aeroacoustic equations and in general any acoustics equations. The governing equations for the motion of a compressible fluid are the continuity equation (mass conservation), the Navier–Stokes equation (momentum conservation), and the general heat transfer equation (energy conservation). In order to close the system of equations, constitutive equations are needed, along with the equation of state, and thermodynamic relations. See, for example, Ref. 3, Ref. 4, Ref. 5, Ref. 6, or Ref. 7 for details and further reading.

where u is the velocity field, ρ is the density, T is the temperature, s is the specific entropy, σ is the stress tensor, q is the local heat flux, Φ is the viscous dissipation function, and M, F, and Q are source terms. The operator D/Dt is the material derivative (or advection operator) defined as

Some thermodynamic relations are necessary when reformulating the energy equations in terms of other sets of thermodynamic variables, like (p, T) or (ρ, p). They are the density differential, the specific energy relation, a relation due to Helmholtz, and the fundamental entropy relation:

where u is the specific internal energy, αp is the coefficient of thermal expansion (isobaric), and βT is the isothermal compressibility. See, for example, Ref. 5 and Ref. 6 for details. They are defined together with the specific heat at constant pressure Cp and specific heat at constant volume Cv as

where k is the thermal conduction, μ is the dynamic viscosity, and μB is the bulk viscosity. This then also defines the viscous dissipation function

In the following, the governing equations are linearized and expanded to first order in the small parameters around the average stationary background solution. For details about perturbation theory see Ref. 3, Ref. 4, and Ref. 8. The small parameter variables (1’st order) represent the acoustic variations on top of the stationary background mean (or average) flow (0’th order solution). Note that, when solving the equations, the value of the acoustic field variables can also represent nonacoustic waves like thermal waves (entropy waves) and vorticity waves. In the time domain, these can be linear instabilities and can actually represent the onset of turbulence.

where A is any of the dependent variables or sources. In the frequency domain, the first order variables are assumed to be harmonic and expanded into Fourier components, such that

The first order variation to material parameters, that are not treated as dependent variables like the density ρ in the Linearized Navier–Stokes interface, is expressed using the density differential and related to perturbations in the temperature and the pressure.