Linearized Navier–Stokes Model

The sets up the governing equations, defines the background mean flow, fluid properties, and the compressibility and thermal expansion properties of the fluid. The governing equations solved are the continuity, momentum, and energy equations:

(5-2)

where pt, ut, and Tt are the acoustic perturbations to the pressure, velocity, and temperature, respectively. The subscript “t” refers to the fact that the acoustic variables are the total fields, that is, the sum of possible Background Acoustic Fields and the scattered fields.

In the frequency domain, the time derivatives of the dependent variables are replaced by multiplication with iω. The stress tensor is σ and Φ is the viscous dissipation function. The right-hand-side source terms M, F, and Q are initially zero; they can be defined using the Domain Sources feature. The variables with a zero subscript are the background mean flow values. The material parameters are defined below. Details about the physics and references are found in the Theory Background for the Aeroacoustics Branch section.

The constitutive equations are the stress tensor and the linearized equation of state, while the Fourier heat conduction law is readily included in the above energy equation,

(5-3)

when is selected in the Linearized Navier–Stokes Equation Settings section the equation of state reduces to

The linearized viscous dissipation function is defined as

(5-4)

Model Inputs

In order to model the influence of the background mean flow on the propagation of the acoustic waves in the fluid, the background mean flow temperature T0, absolute pressure p0, and velocity field u0 need to be defined. The density is defined in the section below, and is per default taken from the material. It is thus a function of the model inputs, that is, the background pressure and temperature. Select (the default) or . For enter values for:

•

T0 (SI unit K). The default is 293.15 K.

•

p0 (SI unit: Pa). The default is 1 atm.

•

u0 (SI unit: m/s). The defaults are 0 m/s.


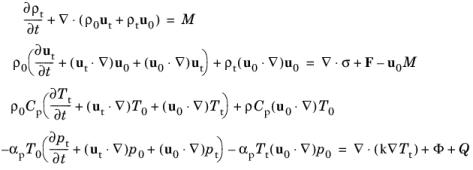
	When modeling aeroacoustics it is important how the Mapping Between Fluid Flow and Acoustics Mesh is done from a numerical perspective. The Background Fluid Flow Coupling multiphysics coupling handles this in an automated manner. Physically the Coupling to Turbulent Flows (Eddy Viscosity) is also important to model the attenuation of acoustics waves due to turbulence.


	Details about the Model Input and the Default Model Inputs are found in the Global and Local Definitions chapter of the COMSOL Multiphysics Reference Manual.

Fluid Properties

The defaults for the following are taken . For edit the default values:

•

ρ0(p0, T0) (SI unit: kg/m3). The option can also be selected as the density formulation.

•

μ (SI unit: Pa·s).

•

μB (SI unit: Pa·s).

•

k (SI unit: W/(m·K)).

•

Cp (SI unit: J/(kg·K)).


	For a discussion about the air and water materials as commonly used in acoustics and other material properties, such as the bulk viscosity, see the Acoustic Properties of Fluids chapter of this manual.

Thermal Expansion and Compressibility

The section is displayed if or is selected as the under the section. For the option the parameters are readily defined.

Select an option from the αp list — , , (the default)or .

Select an option from the βT list — , (the default), or .

The different options for defining the (isobaric) coefficient of thermal expansion and the isothermal compressibility stem from their respective thermodynamic definitions:

•

For the (the default for both) options the values for the c0 (SI unit: m/s) and γ (dimensionless) are taken . For enter a different value or expression. The option is typically preferred (and the default) as the speed of sound and the ratio of specific heats are material properties often more readily available (see definition above).

•

For the the values are computed from the density expression (see definition above). This option is only valid if the density material property has the built in dependency on pressure p0 and temperature T0. This is not always the case.

•

For the the coefficient of thermal expansion is taken from the materials node. Not all materials have this property defined. If this is the case a small warning cross will appear on the materials node.

•

For the option the values for the βs (SI unit: 1/Pa) and γ (dimensionless) are taken (the default). For enter a different values or expressions.

•

For enter a value or expression for the isobaric coefficient of thermal expansion αp (SI unit: 1/K) and/or the isothermal compressibility βT (SI unit: 1/Pa).

Viscous Dissipation Function

Select the check box if you want to include the heat source generated by the viscous losses. The viscous dissipation function Φ is defined in Equation 5-4.

Gradient Term Suppression Stabilization

When the linearized Navier–Stokes (LNS) equations are solved in the time domain (or in the frequency domain with an iterative solver), linear physical instability waves can develop, the so-called Kelvin-Helmholtz instabilities. They are instabilities that can grow, but to less degree than in the linearized Euler equations because losses are present in the LNS equations. They are further naturally limited by nonlinearities in the full Navier–Stokes flow equations. The terms responsible for the instabilities are typically the reactive terms in the governing equations. It has been shown that in some problems the growth of these instabilities can be limited, while the acoustic solution is retained, by canceling terms involving gradients of the mean-flow quantities. This is known as gradient terms suppression (GTS) stabilization.

The GTS option can also be used to alter the governing equations to fit a desired formulation of the linearized Navier–Stokes equations. This can be relevant in certain applications.

All the aeroacoustic specific terms can be disabled. They are grouped into Reactive terms and Convective terms. Select the following check boxes to activate the applicable gradient term suppression (GTS):

Reactive terms

•

This option sets the following term to zero:

•

This option sets the following term to zero:

•

This option sets the following term to zero:

•

This option sets the following term to zero:

Convective terms

•

This option removes all the convective terms in the governing equations. This is a drastic measure as it removes the convective influence of the flow. It should be considered carefully before doing this. This option removes all terms of the type: