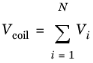The current density flowing in the coil domain is computed from a lumped quantity that constitutes the coil excitation. The choice of this quantity can be done by setting the coil excitation parameter, while the value is specified in the associated text box. All the coil features can be excited either with current excitation, voltage excitation or, in certain cases,
power excitation. The supplied value or expression is translated to a current density or electric field applied to the domain according to the coil model used. Coil features can also retrieve the value of the current or the voltage from a circuit connection, if the parameter coil excitation is set to
Circuit (current) or
Circuit (voltage), respectively.
When specifying a total current Icoil, the coil applies an external electric field in the direction of the current flow, computed as:
where L is equal to the physics interface thickness
d for 2D models,
2πr for 2D axially symmetric models, and the coil length in 3D models.
V is an unknown applied potential. The potential
V is solved for using an additional equation, which constrains the total integrated current to be equal to the current value
Icoil specified, acting as a controller.
When specifying a total current Icoil, the coil applies an external current density in the direction of the wires as in
Equation 3-3 where
N is the number of turns which are specified and
A is the total cross section area of the coil domain.
When specifying a total current Icoil, the out-of-plane component of the current density is defined as:
where L is equal to the physics interface thickness
d for 2D models and
2πr for 2D axially symmetric models, and
V is an unknown applied potential. The potential
V is solved for using an additional algebraic equation, which constrains the total integrated current to be equal to the current value
Icoil specified.
When specifying a total voltage Vcoil, the externally applied electric field is computed as:
where Vcoil is the applied voltage specified, and
L is equal to the physics interface’s thickness
d for 2D models, to
2πr for 2D axially symmetric models, and the coil length in 3D models.
When specifying a voltage Vcoil, the component of the current density in the direction of the wires is defined as in
Equation 3-6 and
Equation 3-7.
where Vcoil is the applied voltage which is specified,
A is the total cross-sectional area of the coil domain,
N is the number of turns specified,
Rcoil is the total resistance of the coil calculated as
where L is equal to the physics interface’s thickness
d for 2D models,
2πr for 2D axially symmetric models, and the coil length in 3D models. The expression
σcoilacoil is the product of the wire bulk conductivity and wire cross-section area.
Vind is the induced voltage calculated by integrating the electric field along the coil.
where Vcoil is the user-defined voltage drop across the coil,
Vi is the individual applied potentials, and
N is the number of turns in the coil group.
When specifying a total voltage Vcoil, the coil applies an out-of-plane external current density computed as:
where Vcoil is the applied voltage specified, and
L is equal to the physics interface’s thickness
d for 2D models and equal to
2πr for 2D axially symmetric models.
In 2D and 2D axisymmetric models, Power is an option available for the coil excitation parameter. When Power is selected, the physics interface sets up the equation as specified in the Current Excitation section, plus a constraint between the coil current and voltage: