The Radiation Pattern plots are available with this module to plot the value of a global variable (for example, the far field norm, normEfar and normdBEfar, or components of the far field variable Efar).

The variables are plotted for a selected number of angles on a unit circle (in 2D) or a unit sphere (in 3D). The angle interval and the number of angles can be manually specified. For 2D Radiation Pattern plots also the reference direction from which the angle is measured and the normal to the plane the far field is computed for can be specified. For 3D Radiation Pattern plots you also specify an expression for the surface color.

The main advantage with the Radiation Pattern plot, as compared to making a Line Graph, is that the unit circle/sphere that you use for defining the plot directions, is not part of your geometry for the solution. Thus, the number of plotting directions is decoupled from the discretization of the solution domain.

1Global maximum variables require the selection for the far-field calculation feature to be spherical for 3D and circular for 2D axisymmetric components and its center to be on the origin.

23D far-field norm functions in 2D axisymmetric geometry are available in these cases:

The function can be used in a 3D Radiation Pattern plot, where the input argument of the function must be same as the Azimuth angle variable in the Evaluation section in the settings window.

The suffix of a function name varies based on the circular port mode type, port mode number and azimuthal mode number in the physics interface. For example, when using azimuthal mode number 1 in the physics interface and transverse electric (TE) mode with mode number 2 in the port settings, the generated operator name is norm3DEfar_TE12.

When the function is used in a radiation pattern plot under a 1D or a polar plot group, the value of input argument defines the plotting plane regardless of the normal and reference direction in the evaluation section in the settings window. For example, norm3DEfar_TE12(0)evaluates the norm of the electric far field for the TE12 mode for 0-degree azimuthal angle. This is equivalent to plotting this variable on the xz-plane. Similarly, norm3DEfar_TE12(pi/2) is the evaluation at 90-degree azimuthal angle, which is equivalent to plotting the variable on the yz-plane.

3The number of input arguments depends on the dimension of model component, 2D, 2D Axisymmetric, or 3D.

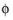
where θ is the elevation angle and is the azimuthal angle.

The uniform two dimensional array factor is simpler than the three dimensional version, as the third, the z-component factor, is unity.

4In the postprocessing expression context menu, far-field functions are available under Component > Definitions > Functions.

While plotting a 3D radiation pattern, the maximum directivity can be calculated by evaluating the ratio between the radiation intensity and the average value of the radiation intensity. Since the radiation intensity is a function of power, the square of the far-field norm has to be used in the Directivity expression in the Radiation Pattern settings window for the antenna directivity calculation. For other physics interfaces, such as in the Acoustics module, the expression is different.

The maximum directivity can be computed through Results > Derived Values > Global Evaluation. This calculation is based on the maximum and averaged intensity values on the far-field calculation selection. It requires the selection for the far-field calculation feature to be spherical for 3D and circular for 2D axisymmetric model components, both centered at the origin.

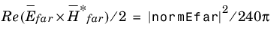
where U is the radiation intensity, and Pin is the total input power.

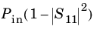
where the delivered power, Pdelivered is . The gain is available only when the S-parameter calculation is valid, that is, for the single port excitation case.