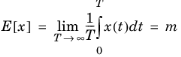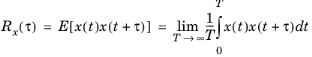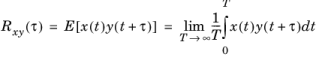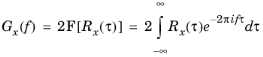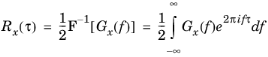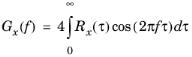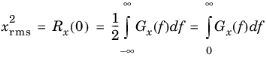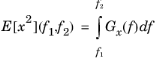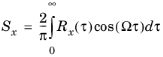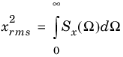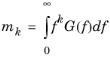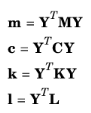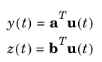Random Vibration Theory
Random vibration analysis is applicable in a situation where the loading has a random variation which can be statistically described by its power spectral density (PSD). The duration of the loading must be such that the situation can be considered as a steady state. The key assumptions are:
•
The system is linear and can be represented by a superposition of a limited number if eigenmodes.
•
The process is ergodic, meaning that its statistical properties do not change over time.
Statistics Preliminaries
Assume a random process x(t). In the following, T denotes a time span which is ‘long’ compared to any frequencies of interest.
The meaning of a ‘long’ time T in this context is that there any vibration mode will experience a large number of cycles. If the lowest frequency of interest is fl, then its corresponding period is Tl = 1/fl. It is then reasonable to require that T > kT, where k is at least 1000, but probably more.
The mean value is defined using the expectancy value operator E[] as
In vibration problems most quantities have zero mean values. Non-linear quantities, like an effective stress, will however have non-zero mean values. Also, if the total effect of a static pre-load and the vibration is considered, the total result will in general have a nonzero mean value.
The variance (the square of the standard deviation) is defined as
The standard deviation is in this context usually called the root mean square (RMS) value of the signal, xrms.
A representation of the ‘degree of similarity over time’ of a signal is given by the autocorrelation function
It can be seen from the definition that the autocorrelation is an even function of the time difference τ. An interpretation of the autocorrelation is that it compares how similar the signal is to itself after a certain time has elapsed.
Also, it can be seen from the definitions above that
For two different processes x(t) and y(t), the cross-correlation is similarly defined as
The power spectral density (PSD) of a signal x is defined through the Fourier transform (denoted by F[]) of the autocorrelation,
The term PSD comes from the fact that the physical dimension of Gx is (input signal)2 / frequency. Thus, Gx(f)Δf represents the power of the signal contained in the small frequency interval Δf.
The inverse relation is
Since the autocorrelation is a real-valued and even function of τ, Gx is also real-valued. Because of this property, Gx can also be written as
The RMS value can be derived from the PSD by integrating the PSD over all frequencies.
It is possible to compute the mean square of x (the power) for only a certain frequency range
This can be interpreted as the energy content of the signal between the two frequencies.
In the same way as for the PSD, the cross spectral density for two signals is defined as
The cross spectral density is in general a complex-valued function, and Gyx is the complex conjugate of Gxy.
It is often more convenient to work with the angular frequency Ω = 2πf, and define the PSD as
so that
and
There are some other scalar statistical properties that can be used to characterize the properties of the spectrum. Define the k:th moment of the spectrum as
The moments can be used to compute the following properties:
•
RMS
•
Average number of (upward) zero crossings per time unit, also called apparent frequency
•
Average number of peaks per time unit
•
Irregularity factor
Transfer Function
For a linear system, the response in the frequency domain for a single variable u to the input x can be written
where H is the complex-valued transfer function. It can then be shown that the corresponding spectral densities have the relation
Here, the superscript ‘*’ denotes complex conjugate. When generalizing to matrices, it denotes the Hermitian conjugate (that is transpose and conjugation).
This type of relation is true not only for the degrees of freedom, but for any quantity that is linearly related to the input. This includes components of stress and (engineering) strain, but not quantities as effective or principal stresses.
When there are multiple input signals (loads), the situation is more complicated. If the inputs are uncorrelated (all cross correlations between them are zero), then the resulting output spectrum can be obtained as a pure superposition of the input spectra weighted by the transfer functions
When the input signals are correlated, the loading must be described by a complete matrix of cross correlation spectra, where the diagonal consists of the individual PSD. Placing the transfer functions from all inputs (N) to all outputs (M) into a rectangular matrix H of size MxN, the operation of computing the output spectral densities and cross correlation spectra can formally be written as
SX is a square matrix having the size of number of inputs, N, while the size of the square matrix SU is the number of outputs, M.
In practice, large sets of output cross-correlation data is uncommon. The most common cases are:
•
Only the diagonal of SU is important. It represents the response of a certain quantity without information about correlation to other quantities. If you are dimensioning a structure, you are interested in the size of the stress, not its covariation with the stress somewhere else.
•
A small set of full correlations are sought. This is the case where the current analysis provides input for another analysis, so that a full spectral input is needed for a number of attachment points.
Modal Representation
The random vibration analysis is implemented based on a mode superposition, encapsulated in a reduced-order model. This approach imposes some limitations:
•
The material data cannot be frequency dependent.
•
There are no non-homogeneous Dirichlet conditions. The common case when there is a fully correlated base excitation can however be handled by shifting the base acceleration into an equivalent gravity load.
In the modal representation, the assumption that the displacements can be described as
where the vector yk contains eigenmode k, and the mode matrix Y has the eigenmodes yk as columns. The modal coordinates (amplitudes of each mode) are collected in the vector q.
Using the common notation that M is the mass matrix, C is the damping matrix and K is the stiffness matrix, the full set equations of motion is
Projecting to the modal base, the corresponding equations are
Lower case matrices is used to indicate a quantity in the modal space.
The projections for the matrices are
In frequency domain, any quantity a can be written using a complex notation as
where â is a complex-valued amplitude. With an assumption about harmonic excitation,
In terms of a transfer function, this can be written as
where
If the applied load is given in terms of its cross-correlation spectra, SL(Ω), then it can be shown that the corresponding cross correlation for the modal loads, Sl(Ω), is obtained by a similar projection into modal space,
Since the number of modes used typically is rather small, the projected cross-correlation matrix is of a manageable size.
It is now possible to compute the cross-correlation spectrum for the modal degrees of freedom as
The cross-correlation spectrum in the physical space is
The spectral distribution of all quantities linearly related to the degrees of freedom can be computed from the modal cross-correlation. Assume that two quantities y(t) and z(t) are linear functions of the degrees of freedom u, so that
Then, by using the definitions above and the linearity of the Fourier transform,