Viscoelastic materials have a time-dependent response even if the loading is constant in time. Many polymers and biological tissues exhibit this behavior. Linear viscoelasticity is a commonly used approximation where the stress depends linearly on the strain and its time derivatives (strain rate). Also, linear viscoelasticity deals with the additive decomposition of stresses and strains. It is usually assumed that the viscous part of the deformation is incompressible so that the volumetric deformation is purely elastic.

For isotropic linear elastic materials in the absence of inelastic stresses, Hooke’s law in Equation 3-11 reduces to

where the elastic strain tensor εel = ε − εinel represents the total strain minus initial and inelastic strains, such as thermal strains.

The elastic strain tensor εel can in the same way be decomposed into volumetric and deviatoric components

The total stress in Equation 3-11 is then

In case of geometric nonlinearity, σ represents the second Piola-Kirchhoff stress tensor and εel the elastic Green-Lagrange strain tensor.

For viscoelastic materials, the deviatoric stress σd is not linearly related to the deviatoric strain εd but it also depends on the strain history. It is normally defined by the hereditary integral:

The function Γ(t) is called the relaxation shear modulus function (or just relaxation function) and it can be found by measuring the stress evolution in time when the material is held at a constant strain.

A physical interpretation of this approach, often called the generalized Maxwell model, is shown in Figure 3-1

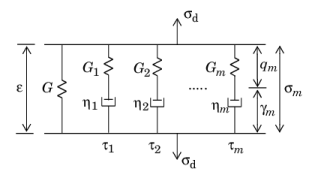
Hence, G is the stiffness of the main elastic branch, Gm represents the stiffness of the spring in branch m, and τm is the relaxation time constant of the spring-dashpot pair in branch m.

The auxiliary strain variable qm is introduced to represent the extension of the corresponding abstract spring, and the auxiliary variables γm = ε − qm represent the extensions in the dashpots.

The shear modulus of the elastic branch G is normally called the long-term shear modulus, or steady-state stiffness, and is often denoted with the symbol G∞. The instantaneous shear modulus G0 is defined as the sum of the stiffness of all the branches

The relaxations time τm is normally measured in the frequency domain, so the viscosity of the dashpot is not a physical quantity but instead it is derived from stiffness and relaxation time measurements. The viscosity of each branch can be expressed in terms of the shear modulus and relaxation time as

The stress per branch can be written either in terms of the strain in the spring qm or the strain in the dashpot γm

The total stress in Hooke’s law (Equation 3-11) is then augmented by the viscoelastic stress σq

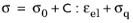
The auxiliary variable γm is a symmetric strain tensor, which has as many components as the number of strain components of the problem class. Since the stress per branch is written as

the auxiliary variables γm can be computed by solving the ODE

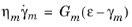
so that Equation 3-23 can equivalently be written as

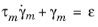
The viscoelastic strain variables γm are treated as additional degrees of freedom. The shape functions are chosen to be one order lower than those used for the displacements because these variables add to the strains and stresses computed from displacement derivatives. The viscoelastic strain variables do not require continuity so discontinuous shape functions are used.

The dissipated energy density rate (SI unit: W/m3) in each branch m is

In order to compute the dissipated energy density, the variable is integrated over time. For frequency domain studies, the dissipation of viscous forces averaged over a time period 2π/ω is computed from the shear loss modulus G'' as

The standard linear solid model, also called SLS model, Zener model, or three-parameter model, is a simplification of the generalized Maxwell model with only one spring-dashpot branch:

where the relaxation time is related to the stiffness and relaxation time as η1 = τ1G1.

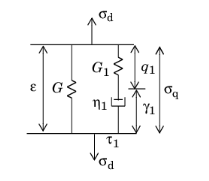
The auxiliary strain tensor γ1 is computed after solving by the ODE

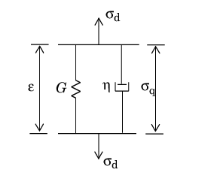
The Kelvin–Voigt viscoelastic model is represented by a spring connected in parallel with a damper:

so there is no need to add the extra DOFs to compute the auxiliary strain tensor γ.

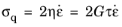
The relaxation time relates the viscosity and shear modulus by η = τG. The equivalent shear modulus is used in case of a anisotropic linear elastic material.

The Burgers model, consists of a spring-dashpot branch in series with a Kelvin-Voigt branch:

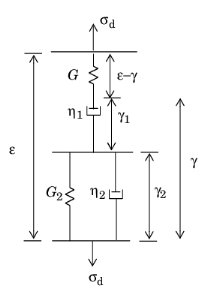
where the shear modulus G is taken from the parent Linear Elastic material.

Combing these equations, it is possible to recover a second-order ODE for the strain tensor γ,

Note that Burgers viscoelastic material has two relaxation times related to the stiffness and viscosity in the springs and dashpots. The relaxation times τ1 and τ2 are related to the stiffness and viscosities as τ1 = η1/G and τ2 = η2/G2.

For many polymers, the viscoelastic properties have a strong dependence on the temperature. A common assumption is that the material is thermorheologically simple (TRS). In a material of this class, a change in the temperature can be transformed directly into a change in the time scale. The reduced time is defined as

where αT(T) is a temperature-dependent shift function.

Think of the shift function αT(T) as a multiplier to the viscosity in the dashpot in the Generalized Maxwell model. This shifts the relaxation time, so Equation 3-24 for a TRS material is modified to

where a base-10 logarithm is assumed. This shift is only valid over a certain range of temperature, typically around the glass transition temperature.

The first step to compute the shift factor αT consists of building a master curve based on experimental data. To do this, the curves of the viscoelastic properties (shear modulus, Young’s modulus, and so forth) versus time or frequency are measured at a reference temperature T0. Then, the same properties are measured at different temperatures.

The shift value of each curve with respect to the master curve obtained at the temperature T0 defines the shift factor αT(T). The constants C1 and C2 are material dependent and are calculated after plotting log(αT) versus T − T0.

Since the master curve is measured at an arbitrary reference temperature T0, the shift factor αT(T) can be derived with respect to any temperature, and it is commonly taken as the shift with respect to the glass transition temperature. The values C1 = 17.4 and C2 = 51.6 K are reasonable approximations for many polymers at this reference temperature.

Below the Vicat softening temperature, the shift factor in polymers is normally assumed to follow an Arrhenius law. In this case, the shift factor is given by the equation

here, a base-e logarithm is assumed, Q is the activation energy (SI unit: : J/mol), and R is the universal gas constant.

The instantaneous shear modulus G0 is defined as the sum of the stiffness of all the branches

Equation 3-22 and Equation 3-24 are then simplified to

where the shear storage modulus G’ and the shear loss modulus G” are defined for the generalized Maxwell model as

The internal work of viscous forces averaged over a time period 2π/ω is computed as