Deformation Measures
Since the deformation tensor F is a two-point tensor, it combines both spatial and material frames. It is not symmetric. Applying a singular value decomposition on the deformation gradient tensor gives an insight into how much stretch and rotation a unit volume of material has been subjected to. The right polar decomposition is defined as
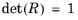
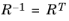
where R is a proper orthogonal tensor (, and ) and U is the right stretch tensor given in the material frame. The rotation tensor R describes the rigid rotation, and all information about the deformation of the material is contained in the symmetric tensor U.
•
The internal variables for the deformation gradient tensor with respect to global material coordinates are named solid.FdxX, solid.FdxY, and so on.
•
The internal variables for the deformation gradient tensor with respect to local material coordinates are named solid.Fdx1, solid.Fdx2, and so on.
•
The rotation tensor components are named solid.RotxX, solid.RotxY, and so on.
•
The right stretch tensor components are named solid.UstchXX, solid.UstchXY, and so on.
An uppercase index refers to the material frame, and a lowercase index refers to the spatial frame.
The stretch tensor contains physically important information about the deformation state. The eigenvalues of the U tensor are the principal stretches, λ1, λ2, and λ3. The stretch of a line element with initial length L0 and current length L is
where εeng is the engineering strain. The three principal stretches act along three orthogonal directions. In the coordinate system defined by these principal directions, the U tensor will be diagonal:
The right Cauchy-Green deformation tensor C defined by
It is a symmetric and positive definite tensor, which accounts for the strain but not for the rotation. The eigenvalues of the C tensor are the squared principal stretches, thus providing a more efficient way to compute the principal stretches than by using the stretch tensor U directly.
The Green-Lagrange strain tensor is a symmetric tensor defined as
Since C is independent of rigid body rotations, this applies also to the Green-Lagrange strain tensor.
Using the displacement components and Cartesian coordinates, the Green-Lagrange strain tensor can be written on component form as
(3-2).
The rotation independence of the Green-Lagrange strain tensor, together with the fact that it for small strain approaches the engineering strain tensor explains why it is a common choice in constitutive models for small strain- finite rotation. As an opposite, a pure rigid rotation causes strains when engineering strains are used.
The Green-Lagrange is the natural strain representation in a Lagrangian description. Since it is a tensor in the material frame, its values should be interpreted in along the undeformed axis orientations.
•
The internal variables for the Green-Lagrange strains are named solid.eX, solid.eXY, and so on.
•
The internal variables for the Green-Lagrange strain tensor in local coordinates are named solid.el11, solid.el12, and so on.
•
In a geometrically linear analysis, the strain variables solid.eX,solid.el11, and so on, will instead represent engineering strain.
•
The right Cauchy-Green deformation tensor in local coordinate system are named solid.Cl11, solid.Cl12, and so on.
Some textbooks prefer to use the left Cauchy-Green deformation tensor B = FFT, which is also symmetric and positive definite but it is defined in the spatial frame.
Engineering Strain
Under the assumption of small displacements and rotations, the normal strain components and the shear strain components are related to the deformation as follows:
(3-3)
In COMSOL Multiphysics, the tensor form of strain representation (εxy, εyz, εxz) is used.
In the documentation, the symbol ε is used to denote strain in general. In a geometrically nonlinear analysis, the strain should be interpreted as a Green-Lagrange strain. In a geometrically linear analysis, the engineering strain is used.
The symmetric strain tensor ε consists of both normal and shear strain components:
The strain-displacement relationships for the axial symmetry case for small displacements are
A special problem occurs at the axis of rotation, where both u and r are zero. To avoid dividing by zero, the circumferential strain is for very small values of r redefined to
The alternative expression is obtained by applying L’Hôpital’s rule.
A general description of the axially symmetric case is given in Axial Symmetry and Deformation.
Logarithmic Strain
The logarithmic strain, also called true strain, or Hencky strain, is a popular strain measure for large strain, in particular when representing data from tensile tests. For a uniaxial case, it is defined on the incremental form
where L is the current length of the specimen. If this relation is integrated, the total strain can be written as
Here L0 is the initial length and λ is the stretch.
In order to generalize the logarithmic strain to a strain tensor, it is necessary to first compute the three principal stretches and their orientation. Then, a logarithmic strain tensor in the local principal stretch system is defined as
This tensor is then transformed to the global coordinate system in order to give the logarithmic strain tensor.