Dependent Variables
The element used for the shell interface is of Mindlin-Reissner type, which means that transverse shear deformation is accounted for. It can thus also be used for rather thick shells. In 3D and for plates, an MITC (mixed interpolation of tensorial components) formulation is used. A general description of this element family is given in Ref. 1.
The dependent variables in 3D are the displacements u, v, and w in the global x, y, and z directions, and the displacements of the shell normals ax, ay, and az in the global x, y, and z directions.
Figure 5-1: The degrees of freedom in the shell interface. N is the normal vector in the original configuration and n is the normal in the deformed state.
The degrees of freedom represent the displacements on the reference surface. If an offset property is used, the reference surface differs from the physical shell midsurface. The displacement vector on the midsurface, u, can be expressed as
where uR is the displacement on the reference surface (the displacement degrees of freedom) and ζ0 is the offset. The rotational displacement a is the same on both midsurface and reference surface.
In axisymmetry, there are four degrees of freedom, since u and a only has components in the RZ-plane.
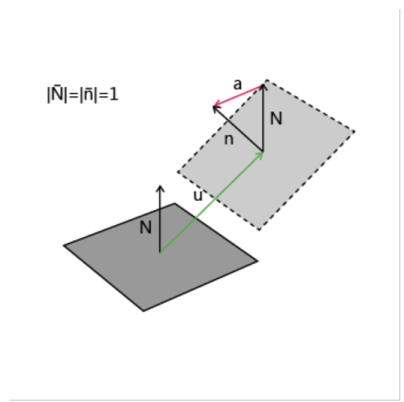
For input and output, the Shell interface to a large extent replaces the displacements of the shell normals by the more customary rotations θx, θy, and θz about the global axes. For a geometrically linear analysis, the relation between normal displacement and rotation vector is simple: a = θ × n where n is the unit normal of the shell.
For a standard plate analysis only three degrees of freedom are needed: the out-of-plane displacement w and the displacements of the shell normals ax and ay. It is also possible to activate all six degrees of freedom, so that any type of analysis of a shell initially positioned in the xy-plane can be performed using the Plate interface. Using six degrees of freedom is the default, but three degrees of freedom can be selected instead for efficiency.
Also for plates, the rotations θx, θy, and (possibly) θz are used to a large extent.
•
When six degrees of freedoms are used in the Plate interface, there must be enough constraints to suppress any in-plane rigid body motions.
•
In the Shell interface, the coordinates are usually denoted with lowercase letters (x, y, z). If a Solid Mechanics or Membrane interface is present in the same model, then it becomes necessary to make a difference between the material frame and the spatial frame (Material and Spatial Coordinates). In this case, the coordinates in the Shell interface changes to (X, Y, Z).