A common method of modeling damping is Rayleigh damping, where two damping coefficients are specified. This type of damping is not directly related to any physical process, but must be seen as a way to take the total damping of a structure into account.

Rayleigh damping introduces damping in a form based on Equation 2-20. This means that the method can be applied generally in either the time or frequency domain. The parameter c in Equation 2-20 is defined as a fraction of the mass and the stiffness using two parameters, αdM and βdK, such that

Substituting this relationship into Equation 2-20 and rearranging into the form of Equation 2-21 gives:

When there are many degrees of freedom m, k, and c become matrices and the technique can be generalized.

Note that Equation 2-25 holds separately for each vibrational mode in the system at its resonant frequency. In the frequency domain it is possible to use frequency dependent values of αdM and βdK. For example setting αdM = 0 and βdK = 2ζ/ω0 produces a equivalent viscous damping model at the resonant frequency.

While Rayleigh damping is numerically convenient, the model does not agree with experimental results for the frequency dependence of material damping over an extended range of frequencies. This is because the material damping forces behave more like frictional forces (which are frequency independent) than viscous damping forces (which increase linearly with frequency as implied by Equation 2-22). In the frequency domain it is possible to introduce loss factor damping, which has the desired property of frequency independence.

A complication with the Rayleigh damping model is to obtain good values for the damping parameters αdM and βdK. A more physical damping measure is the damping ratio, the ratio between actual and critical damping, often expressed as a percentage of the critical damping. Commonly used values of the damping ratio can be found in the literature.

Using Equation 2-25, this relationship at two frequencies, f1 and f2, with different damping ratio, ζ1 and ζ2, results in an equation system that can be solved for αdM and βdK:

Using the same damping ratio, ζ1 = ζ2, does not result in a constant damping factor inside the interval f1 < f < f2. It can be shown that the damping factor is lower inside the interval, as Figure 2-13 shows.

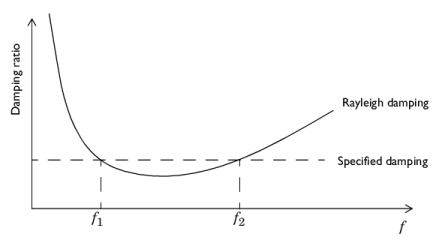
Since the coefficients αdM and βdK. should not be negative, the damping ratios are constrained by the respective frequencies as

For many applications it is sufficient to leave αdM as zero and to define damping only using the βdK coefficient. Then according to Equation 2-25, a damping which increases linearly with frequency is obtained. If the damping ratio ζ(f0) or loss factor η(f0) is known at a given frequency f0, the appropriate value for βdK is: