You are viewing the documentation for an older COMSOL version. The latest version is
available here.
Reduced-order modeling seeks to reduce the number of degrees of freedom in a physical model, whilst still retaining the essential physics. For a lightly damped resonant system driven at one of its resonant frequencies, it is reasonable to consider only the contributions to the system of a small number (m) of modes within the signal bandwidth. In some cases, a single mode is sufficient. A system with
n degrees of freedom has mass, stiffness, and damping matrices of size
n-by-
n. A reduced-order representation of the system considering
m modes has size
m-by-
m. The reduction in complexity of the system, and the computational speed up is therefore significant when
m «
n. This section describes the theory of the reduced-order system and gives guidelines on how to obtain reduced-order models from a COMSOL model.
Consider a mechanical system, with n degrees of freedom, described by an equation of the form
(2-5)
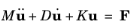
where u is the displacement vector (size:
n-by-1),
K is the stiffness matrix (size:
n-by-
n),
D is the damping matrix (size:
n-by-
n), and
M is the mass matrix (size:
n-by-
n). In the frequency domain the problem takes the form
(2-6)
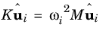
(2-7)

(2-8)

Next the following n-by-
n matrix is constructed, with columns taken from the
n eigenvectors:
From Equation 2-7 it is clear that this is a diagonal matrix. Similarly from
Equation 2-8 it is clear that
UTKU is also diagonal.
(2-9)
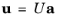
where a is a column vector containing the coefficients
ai as rows. In general
a is time-dependent.
Now consider the original equation: Equation 2-5. First substitute for
u using
Equation 2-9. Then transform the equation to the
modal coordinate system by premultiplying by
UT. This gives:
(2-10)
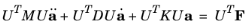
It has already been established that the matrices UTMU and
UTKU are diagonal and frequently a damping model is chosen that results in a diagonal damping matrix. For example, in Rayleigh damping
D = αM + βK, where
α and
β are constants. For a general damping, the transformed damping matrix is however not diagonal. As an alternative, a damping ratio,
ζi, can be assigned to each mode.
The precise form of Equation 2-10 is determined by the normalization adopted for the eigenfunctions. In structural applications the eigenfunctions are often normalized such that
UTMU = I. This is referred to as
mass matrix scaling in the eigenvalue solver. In this case
Equation 2-6 gives
where diag(ωi2) is the diagonal matrix with diagonal elements
ωi2. Similarly, if damping ratios for each mode are defined, the damping matrix can be expressed in the form
Thus if mass matrix scaling is used
Equation 2-10 takes the form
(2-11)
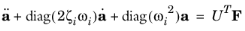
It is also possible to scale the eigenvectors so that the point of maximum displacement has unit displacement. This is referred to as max scaling in the eigenvalue solver. For an individual mode this scaling has a simple physical interpretation — the corresponding component of
a,
ai, is the amplitude of the
ith mode, measured at the point of maximum displacement, when the mode is driven by the force
F. In this case
Equation 2-10 takes the form
(2-12)
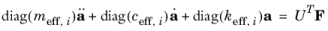
Here meff,i is the effective mass of the
ith mode,
ceff,i = 2meff,iξiωi is the effective damping parameter for the mode, and
keff,i is the effective spring constant. Each element of the vector
UTF gives the force component that acts on each of the respective modes.
The expression for u in matrix becomes:
where U' is now an
m-by-
n and
a' is a vector with
m components. The equation system in modal coordinates now takes the form
(2-13)
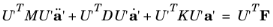
The matrices U'TMU',
U'TDU', and
U'TKU' now have dimensions
m-by-
m. Similarly the vector
U'TF has
m components. This results in a significant reduction in the system complexity.
where U'r is the
n-by-
m matrix containing the right eigenvectors chosen for the modal analysis. Once again
a' is a vector with
m components. The system in modal coordinates takes the form
where U'l is the
n-by-
m matrix containing the left eigenvectors chosen for the modal analysis.
The matrices U'lTMU'r,
U'lTDU'r, and
U'lTKU'r are no longer necessarily diagonal. The modal solver accepts any linearly independent set of vectors to project the solution vector and equations onto and constructs the reduced-order system accordingly.
The Model Reduction and
Modal Reduced Order Model study steps have the property that they can assemble the modal matrices and make them available for output. In the
Model Reduction node, the
Store reduced matrices check box must be selected.
After the model has solved, right-click the Results>Derived Values node and select
System Matrices. In the output section choose the
Matrix to display in the list. The mass matrix corresponds to the matrix
U'lTMU'r the stiffness matrix corresponds to
U'lTKU'r, and the damping matrix corresponds to
U'lTDU'r. The vector
U'lTF is available as the load vector. These matrices are given in a format that respects the normalization of the preceding
Eigenvalue Solver. To change this select the
Eigenvalue Solver node, and change the
Scaling of Eigenvectors setting under the
Output section. Use the
Max setting if an equivalent Mass-Spring-Damper system is required, in which case the modal amplitude corresponds to the maximum displacement of the mode.