The thickness of the membrane is d, which can vary over the element. The displacements are interpolated by Lagrange or Serendipity shape functions.

This local membrane surface coordinate system is defined by the boundary coordinate system (t1, t2, n).

The deformation gradient F is in general defined as the gradient of the current coordinates with respect to the original coordinates:

Here 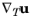is a displacement gradient computed using the tangential derivative operator, and N is the normal vector to the undeformed membrane. FT now contains information about the stretching in the plane of the membrane.

Since the tangential deformation gradient does not contain any information about the transversal stretch λn, it must be augmented by the normal deformation gradient FN to define the full deformation gradient tensor. It is given by

where n is the normal vector to the deformed membrane. For anisotropic materials, the shear deformation gradient FS is also necessary to define the full deformation gradient tensor. It is given by

where t1 and t2 are the tangent vectors to the deformed membrane. The full deformation gradient tensor F is the sum of tangential, shear and normal deformation gradient tensors

Note that FS is only nonzero for anisotropic materials, otherwise FS = 0.

The Right Cauchy-Green tensor C is generally defined as

From C, the Green-Lagrange strains are computed using the standard expression

In the membrane, only the C tensor is available, so instead the following expression is used:

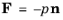
where the forces (F) can be distributed over a boundary or an edge or be concentrated in a point. In the special case of a follower load, defined by its pressure p, the force intensity is where n is the normal in the deformed configuration.