Use the Release node to release rays within domains based on arbitrary expressions or based on the positions of the mesh elements.

This section is only available when the Allow multiple release times check box has been selected in the physics interface Advanced Settings section. Enter Release times (SI unit: s) or click the Range button () to select and define a range of specific times. At each release time, rays are released with initial position and ray direction vector as defined next.

Select an Initial position: Density (the default) or Mesh based.

For Density enter a value for the Number of rays per release N (dimensionless). The default is 100. Then enter a value or expression for the Density proportional to ρ (dimensionless). The default is 1.

The Density proportional to ρ can be an expression rather than a number; the resulting ray distribution approximately has a number density that is proportional to this expression. The resulting distribution looks a bit random, and it depends on the order in which the mesh elements are numbered. The distribution is probably not exactly the same in different COMSOL Multiphysics versions, but the total number of rays released is always N.

The following options can be adjusted to make the number density of rays more closely conform to the Density proportional to expression.

Select a Release distribution accuracy order between 1 and 5 (the default is 5), which determines the integration order that is used when computing the number of rays to release within each mesh element. The higher the accuracy order, the more accurately rays will be distributed among the mesh elements.

The Position refinement factor (default 0) must be a nonnegative integer. When the refinement factor is 0, each ray is always assigned a unique position, but the density is taken as a uniform value over each mesh element. If the refinement factor is a positive integer, the distribution of rays within each mesh element is weighted according to the density, but it is possible for some rays to occupy the same initial position. Further increasing the Position refinement factor increases the number of evaluation points within each mesh element to reduce the probability of multiple rays occupying the same initial position.

For Mesh based the rays are released from a set of positions determined by a selection of geometric entities (of arbitrary dimension) in the mesh. Given a Refinement factor between 1 and 5, the centers of the refined mesh elements are used. Thus, the number of positions per mesh element is refine^dim, except for pyramids, where it is (4*refine2-1)*refine/3.

Select an option from the Ray direction vector list: Expression (the default), Spherical, Hemispherical, Conical, or Lambertian (3D only).

If Conical is selected, select an option from the Conical distribution list: Uniform density (the default), Specify polar and azimuthal distributions, Hexapolar, Marginal rays only, or Marginal and axial rays only.

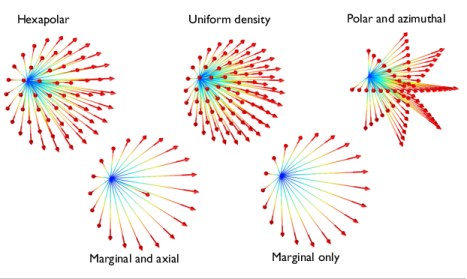
For Spherical, Hemispherical, Conical, and Lambertian, select an option from the Sampling from Distribution list: Deterministic (the default) or Random. If Deterministic is selected, the initial ray direction vectors are computed using an algorithm that seeks to distribute the rays as evenly as possible in wave vector space. This algorithm will give the same initial ray directions whenever the study is run. If Random is selected, the initial direction of each ray is sampled from a probability distribution in wave vector space using pseudorandom numbers. The result may be the same when rerunning the study multiple times on the same computer, but the solution is likely to be different on different architectures.

This section is available when Polychromatic, specify frequency is selected from the Wavelength distribution of released rays list in the physics interface Ray Release and Propagation section.

Select a Distribution function: None (the default), Normal, Lognormal, Uniform, or List of values.

When None is selected, enter an initial value ν0 (SI unit: Hz). The default value is 4.54 × 1014 Hz.

Select Normal to create a normal distribution function, Lognormal to create a log-normal distribution function, or Uniform to create a uniform distribution function. For any of these selections, the Number of values sets the number of points in the distribution function. Enter a user-defined Mean (default 4.54 × 1014 Hz) and Standard deviation (default 1014 Hz). Select List of values to enter a list of distinct frequency values.

This section is available when Polychromatic, specify vacuum wavelength is selected from the Wavelength distribution of released rays list in the physics interface Ray Release and Propagation section.

Select a Distribution function: None (the default), Normal, Lognormal, Uniform, or List of values.

When None is selected, enter a value or expression for the Vacuum wavelength λ0 (SI unit: m). The default is 660 nm. All rays released by this feature will have the same wavelength.

Select Normal to create a normal distribution function, Lognormal to create a log-normal distribution function, or Uniform to create a uniform distribution function. For any of these selections, the Number of values sets the number of points in the distribution function. Enter a user-defined Mean (default 660 nm) and Standard deviation (default 100 nm). Select List of values to enter a list of distinct wavelength values directly.

This section is available when the Compute phase check box is selected under the physics interface Intensity Computation section. Enter an Initial phase Ψ0 (SI unit: rad). The default value is 0.

This section is available when the ray intensity is solved for in the model and Expression is selected as the Ray direction vector. Enter a value for the Initial intensity I0 (SI unit: W/m2). The default is 1000 W/m2.

This section is available when the ray intensity is solved for in the model and Expression is selected as the Ray direction vector. Select a Wavefront shape. In 3D the available options are Plane wave (the default), Spherical wave, and Ellipsoid. In 2D the available options are Plane wave (the default) and Cylindrical wave.

Select an Initial polarization type: Unpolarized (the default), Fully polarized, or Partially polarized.

Select an Initial polarization: Along principal curvature direction (the default) or User defined.

For Partially polarized, also enter an Initial degree of polarization P0 (dimensionless).

Select an option from the Intensity initialization list. By default Uniform distribution is selected. If any Photometric Data Import nodes have been added to the model then they can also be selected from the list.

If Uniform distribution is selected, enter a Total source power Psrc (SI unit: W). The default is 1 W. In 2D, instead enter the Total source power per unit thickness Psrc (SI unit: W/m). The default is 1 W/m. If any Photometric Data Import feature is selected from the list, the source power is instead obtained directly from the imported photometric data (IES) file. Enter values or expressions for the components of the Photometric horizontal ph (dimensionless) and Photometric zero pz (dimensionless). By default, these vectors point in the directions of the positive x- and z-axes, respectively.

For each of the Auxiliary Dependent Variable nodes added to the model, select a Distribution function for the initial value of the auxiliary dependent variables and whether the initial value of the auxiliary dependent variables should be a scalar value or sampled from a distribution function.

The number of rays simulated can increase substantially and the following options are available for each Auxiliary Dependent Variable added to the model.

When None is selected, enter an initial value. The symbol for the initial value is the auxiliary variable name followed by a subscript 0, so for the default name rp the initial value has symbol rp0.

For the initial value of the auxiliary dependent variables, select Normal to create a normal distribution function, Lognormal to create a log-normal distribution function, or Uniform to create a uniform distribution function. For any selection, the Number of values sets the number of points in the distribution function. Enter a user-defined Mean (default 0) and Standard deviation (default 1). Select List of values to enter a set of numerical values directly.

By default auxiliary dependent variables are initialized after all other degrees of freedom. Select the Initialize before wave vector check box to compute the initial value of the auxiliary dependent variable immediately after computing the initial wave vectors of the rays. By selecting this check box it is possible to define the initial ray direction as a function of the auxiliary dependent variables.