Frequency Domain Equation
Writing the fields on a time-harmonic form, assuming a sinusoidal excitation and linear media,
the two laws can be combined into a time harmonic equation for the electric field, or a similar equation for the magnetic field
The first of these, based on the electric field is used in The Electromagnetic Waves, Frequency Domain Interface.
Using the relation εr = n2, where n is the refractive index, the equation can alternatively be written
The wave number in vacuum k0 is defined by
where c0 is the speed of light in vacuum.
When the equation is written using the refractive index, the assumption is that μr = 1 and σ = 0 and only the constitutive relations for linear materials are available. When solving for the scattered field the same equations are used but E = Esc + Ei and Esc is the dependent variable.
Eigenfrequency Analysis
When solving the frequency domain equation as an eigenfrequency problem the eigenvalue is the complex eigenfrequency λ = jω + δ, where δ is the damping of the solution. The Q-factor is given from the eigenvalue by the formula
Mode Analysis and Boundary Mode Analysis
In mode analysis and boundary mode analysis COMSOL Multiphysics solves for the propagation constant. The time-harmonic representation is almost the same as for the eigenfrequency analysis, but with a known propagation in the out-of-plane direction
The spatial parameter, α = δz + jβ = −λ, can have a real part and an imaginary part. The propagation constant is equal to the imaginary part, and the real part, δz, represents the damping along the propagation direction. When solving for all three electric field components the allowed anisotropy of the optionally complex relative permittivity and relative permeability is limited to:
Limiting the electric field component solved for to the out-of-plane component for TE modes requires that the medium is homogeneous; that is, μ and ε are constant. When solving for the in-plane electric field components for TM modes, μ can vary but ε must be constant. It is strongly recommended to use the most general approach, that is solving for all three components which is sometimes referred to as “perpendicular hybrid-mode waves”.
Variables Influenced by Mode Analysis
The following table lists the variables that are influenced by the mode analysis:
Name
Expression
Can be Complex
Description
beta
imag(-lambda)
No
Propagation constant
dampz
real(-lambda)
No
Attenuation constant
dampzdB
20*log10(exp(1))*dampz
No
Attenuation per meter in dB
neff
j*lambda/k0
Yes
Effective mode index
Propagating Waves in 2D
In 2D, different polarizations can be chosen by selecting to solve for a subset of the 3D vector components. When selecting all three components, the 3D equation applies with the addition that out-of-plane spatial derivatives are evaluated for the prescribed out-of-plane wave vector dependence of the electric field.
In 2D, the electric field varies with the out-of-plane wave number kz as
.
The wave equation is thereby rewritten as
,
where z is the unit vector in the out-of-plane z direction.
Similarly, in 2D axisymmetry, the electric field varies with the azimuthal mode number m as
and the wave equation is expressed as
,
where is the unit vector in the out-of-plane  direction.
In-plane Hybrid-Mode Waves
Solving for all three components in 2D is referred to as “hybrid-mode waves”. The equation is formally the same as in 3D with the addition that out-of-plane spatial derivatives are evaluated for the prescribed out-of-plane wave vector dependence of the electric field
In-plane TM Waves
The TM waves polarization has only one magnetic field component in the z direction, and the electric field lies in the modeling plane. Thus the time-harmonic fields can be obtained by solving for the in-plane electric field components only. The equation is formally the same as in 3D, the only difference being that the out-of-plane electric field component is zero everywhere and that out-of-plane spatial derivatives are evaluated for the prescribed out-of-plane wave vector dependence of the electric field.
In-plane TE Waves
As the field propagates in the modeling xy-plane a TE wave has only one nonzero electric field component, namely in the z direction. The magnetic field lies in the modeling plane. Thus the time-harmonic fields can be simplified to a scalar equation for Ez,
where
To be able to write the fields in this form, it is also required that εr, σ, and μr are nondiagonal only in the xy-plane. μr denotes a 2-by-2 tensor, and εrzz and σzz are the relative permittivity and conductivity in the z direction.
Axisymmetric Hybrid-Mode Waves
Solving for all three components in 2D is referred to as “hybrid-mode waves”. The equation is formally the same as in 3D with the addition that spatial derivatives with respect to  are evaluated for the prescribed azimuthal mode number dependence of the electric field.
Axisymmetric TM Waves
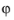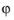
A TM wave has a magnetic field with only a  component and thus an electric field with components in the rz-plane only. The equation is formally the same as in 3D, the only difference being that the  component is zero everywhere and that spatial derivatives with respect to  are evaluated for the prescribed azimuthal mode number dependence of the electric field.
Axisymmetric TE Waves
A TE wave has only an electric field component in the  direction, and the magnetic field lies in the modeling plane. Given these constraints, the 3D equation can be simplified to a scalar equation for . To write the fields in this form, it is also required that εr and μr are nondiagonal only in the rz-plane. μr denotes a 2-by-2 tensor, while and are the relative permittivity and conductivity in the  direction.
Introducing Losses in the Frequency Domain
Electric Losses
The frequency domain equations allow for several ways of introducing electric losses. Finite conductivity results in a complex permittivity,
The conductivity gives rise to ohmic losses in the medium.
A more general approach is to use a complex permittivity,
where ε' is the real part of εr, and all losses (dielectric and conduction losses) are given by ε''. The dielectric loss model can also single out the losses from finite conductivity (so that ε'' only represents dielectric losses) resulting in:
The complex permittivity can also be introduced as a loss tangent:
When specifying losses through a loss tangent, conductivity is not allowed as an input.
In optics and photonics applications, the refractive index is often used instead of the permittivity. In materials where μr is 1, the relation between the complex refractive index
and the complex relative permittivity is
that is
The inverse relations are
The parameter κ represents a damping of the electromagnetic wave. When specifying the refractive index, conductivity is not allowed as an input.
In the physics and optics literature, the time harmonic form is often written with a minus sign (and “i” instead of “j”):
This makes an important difference in how loss is represented by complex material coefficients like permittivity and refractive index, that is, by having a positive imaginary part rather than a negative one. Therefore, material data taken from the literature might have to be conjugated before using it in a model.
Magnetic Losses
The frequency domain equations allow for magnetic losses to be introduced as a complex relative permeability.
The complex relative permeability can be combined with any electric loss model except refractive index.