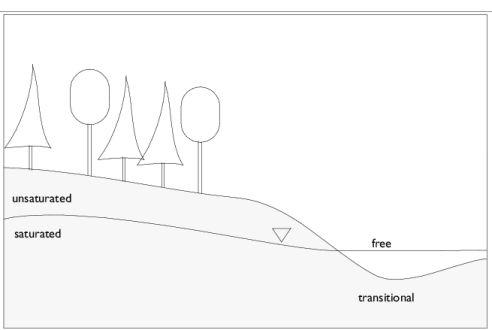
Figure 3-1 illustrates typical settings where the various flow regimes apply.
Here s represents a location on the streamline,
u denotes the fluid velocity,
ρf is the fluid density,
p refers to the fluid pressure,
g represents gravity, and
D is the elevation. The Bernoulli equation states that the total mechanical energy is constant along the fluid trajectory in a steady flow system. Moreover, the energy can shift between velocity, pressure, and elevation along the streamline.

