Corona Discharges Theory
Coronas are weakly luminous self-sustained discharges, which appears near sharp points, edges, or thin wires where the electric field is much more intense than in the rest of the gap Ref. 1. The appearance of corona discharges is explained by physical mechanisms of electron creation in the region of intense electric field where ionization occurs. The creation mechanism of electrons depends on the polarity of the corona electrode. In the case the electrode is a cathode the corona is called negative corona and the discharge ignition is analogous to a Townsend breakdown due to secondary emission from the cathode
(2-3)
where α and η are the ionization and attachment Townsend coefficients, γ is the secondary electron emission coefficient, and the integration is between the cathode and the positions xm where α(xm)=η(xm). In the case the electrode is a anode the corona is called positive corona and the ignition mechanism is related to cathode-directed streamers described by the generalized Meek breakdown criterion
(2-4).
However the value of the integral in Equation 2-3 is about 2 times smaller than the one in Equation 2-4, the value of the breakdown electric field is only slight different because of the steep dependence of the Townsend coefficients with the electric field.
Equation 2-3 and Equation 2-4 can be used to find a lower limit for the electric field at the corona electrode above which there is gas breakdown. However, instead of solving the integrals above a common approach to estimate the breakdown electric field in corona discharges is to use empirical expressions of the type proposed by Peek. For coaxial type coronas, Peek proposed the following expression for the breakdown in air
(2-5)
where E0 (SI unit: V/m) is the breakdown electric field, δ is the gas number density normalized to the gas density at 760 Torr and 293.15 K, and ri is the radius of the corona electrode. This expression can be adapted to other gases and geometries by adjusting the numerical coefficients.
The creation of charge carriers occurs only in a region very close to the corona electrode where the electric fields are very intense. In the remainder of the gap, charged carriers are transported in a weak electric field thus closing the circuit. In the transport region the charge carriers are positive ions in the positive corona and negative ions in the negative corona. If the gas is only weekly electronegative there can be electrons as well.
The physics of coronas ignition and maintenance is rather complicated to describe numerical since it involves cathode fall, streamers, and photo-ionization. The model described in this section aims to bypass all this complex physics by providing suitable boundary conditions. In practice, a potential and a electric field are imposed at the corona electrode and the model uses a charge conservation equation to describe the transport region of a corona where only one type of charge carrier exits (i.e. positive or negative ions).
In this type of models, to justify a boundary condition where an electric field and a potential are imposed at the corona electrode, it is used Kaptsov’s hypothesis that says that the electric field at the corona electrode after the discharge breakdown is independent of the applied voltage and stays fixed at that value Ref. 2.
Domain equations
The model is based on the conservation of current transported by the charged carriers. It should be emphasized that the model is not self-consistent in the sense that both potential and the electric field need to be given at the corona electrode. In other words, the electric field necessary to sustain the discharge is not obtained from first principles: electron and ion transport, electrons gaining energy from the electric field, and electrons losing energy in collisions with the background gas.
The space charge density and the electrostatic potential are solved using the charge conservation, current density, and Poisson’s equations Ref. 2
(2-6)
(2-7)
(2-8)
where:
•
J is the current density (SI unit: C/m2).
•
ρ is the space charge density (SI unit: C/m3).
•
S is the current source (SI unit: C/m3).
•
Zq is the charge number (SI unit: 1).
•
E is the electric field (SI unit: V/m).
•
V is the electric field (SI unit: V/m).
•
μi is the ion mobility (SI unit: m2/(V.s)).
•
u is the neutral fluid velocity vector (SI unit: m/s).
Equation 2-6, Equation 2-7, and Equation 2-8 are manipulated to obtained a single equation for the space charge density
(2-9)
that is solved coupled with Poisson’s equation.
Boundary conditions
In the corona model presented here, as discussed above, the boundary conditions at the corona electrode are unusual and consists of giving a electric field and a potential at the corona electrode. The normal component of the electric field at the corona electrode is used as a boundary condition for Poisson’s equation
(2-10).
The boundary condition for Equation 2-9 involves in finding the space charge density at the corona electrode, using a Lagrange multiplier, so that the imposed potential V0 is verified
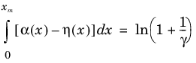
(2-11).
Since the field and potential are not found self-consistently their values need to have physical meaning in order to represent a corona discharge.
 
When changing the polarity of the corona make sure that the electric field and potential at the electrode (defined in the Electrode multiphysics coupling), the sign of the charge number of the charge carriers (defined in the Transport Properties feature in the Charge Transport interface) and the sign of the initial value of the space charge density (defined in the Initial Values feature of the Charge Transport interface) are coherent.