You are viewing the documentation for an older COMSOL version. The latest version is
available here.
The Newtonian formulation is the default and the most common formulation. It defines a set of second-order ordinary differential equations for the components of the particle position based on Newton’s second law of motion,
where q (SI unit: m) is the particle position,
mp (SI unit: kg) is the particle mass, and
F (SI unit: N) is the total force on the particles.
The Newtonian, first order formulation is an alternative to the
Newtonian formulation. It defines a set of coupled first-order ordinary differential equations for the components of the particle position and velocity,
The default time stepping method for the first-order Newtonian formulation is the Dormand-Prince 5 Runge-Kutta method, an explicit time stepping method. By comparison, the second-order Newtonian formulation uses the
Generalized alpha implicit method by default.
The explicit time stepping method is less suitable for stiff problems, meaning that the Newtonian formulation is more robust when the particles are subjected to extremely large, abrupt accelerations. The
Newtonian formulation is also favorable for problems involving ultrarelativistic particles. However, for some nonstiff problems, the explicit method can give comparable or even better accuracy and performance, compared to the implicit method.
Generally, it is most convenient to begin with the default Newtonian formulation, then to consider switching to the
Newtonian, first order formulation to optimize performance if the problem is not overtly stiff.
The Massless formulation defines a set of first-order ordinary differential equations for the components of the particle position only. The particle velocity is directly specified, either by an expression of by using a previously computed field.
The Massless formulation is useful for modeling the motion of extremely small particles in a fluid. If Brownian diffusion and turbulent dispersion are neglected, the ratio of the drag force to the mass of an extremely small particle is often so large that the particle reaches equilibrium with the surrounding flow almost instantaneously, so that the particles follow fluid streamlines. Such particles are sometimes referred to as
tracer particles, as opposed to
inertial particles which are allowed to have some nonzero velocity relative to the fluid.
The Lagrangian formulation (
Ref. 2, Chapter 1) defines a set of second-order ordinary differential equations for the components of the particle position. Compared to the
Newtonian formulation, the
Lagrangian formulation has the same number of degrees of freedom and offers greater flexibility in specifying the equations of motion, but it is not possible to use the
Force feature.
(2-1)
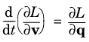
where v (SI unit: m/s) is the particle velocity and
q (SI unit: m) is the particle position.
Equation 2-1 is called the
Euler-Lagrange equation.
(2-2)
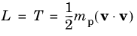
For example, for an instance of The Mathematical Particle Tracing Interface with tag
pt in 3D, the expression
pt.mp*(pt.vx^2+pt.vy^2+pt.vz^2)/2 is the Lagrangian for a free particle that is not subjected to any forces. Note that substitution into the Euler-Lagrange equation yields
where T (SI unit: J) is the particle kinetic energy and
U (SI unit: J) is the total potential energy. For example, if
U only depends on particle position, not velocity, then substitution into the Euler-Lagrange equation yields
Following Chapter 7 in Ref. 2 the Hamiltonian
H (SI unit: J) can be derived directly from an expression for the Lagrangian
L. The degrees of freedom are the position vector components
qi and the
generalized momenta pi, defined as
(2-3)
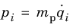
for i from
1 to the total number of space dimensions. Thus, in this case the generalized momentum is simply the particle momentum.
(2-4)
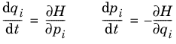
These are known as Hamilton’s equations.
For example, for an instance of The Mathematical Particle Tracing Interface with tag
pt in 3D, using default names for the generalized momentum components, the expression
(px^2+py^2+pz^2)/(2*pt.mp) is the Hamiltonian for a free particle that is not subjected to any forces. Substitution into Hamilton’s Equations then yields