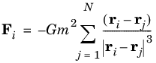Particle-Particle Interaction

	The Particle-Particle Interaction node is only available when Newtonian or Newtonian, first order is selected as the Formulation in the physics interface Particle Release and Propagation section. This feature does not support hard sphere collisions; the interaction forces must be finite and must be expressed as continuous functions of the distance between particles.

Use the node to make particles exert forces on each other. There are predefined options available for the Coulomb, Lennard-Jones, and linear elastic forces. It is also possible to define arbitrary expressions for the interaction force.

Select an option from the list: (the default), , , or . If the default, , is kept, a Coulomb force describes the interaction between charged particles. No user input is necessary.

For enter the ks (SI unit: N/m). The default is 1 N/m. Enter the r0 (SI unit: m). The default is 1 mm.

For it uses the Lennard-Jones potential to approximate the interaction between neutral particles. The value of these parameters depend on the gas molecules interacting and can usually be found from a literature search.

•

Enter the σ (SI unit: m), typically in the order of a few angstroms (the default value is 3.3 × 10−10 m or 3.3 Å).

•

Enter the ε (SI unit: J), usually in the order of 10−21 J (the default value is 1.6 × 10−21 J).

	There is specific syntax that you must use to specify user-defined interaction forces.

For enter a user-defined expression for the interaction Fu (SI unit: N) based on space dimension.

The particle degrees of freedom are given the variable names qx, qy, and qz (in 3D), but to access the position vector of neighboring particles use the expression dest(qx), dest(qy), and dest(qz).

A predefined expression for the distance between particles is available because the particle-particle interaction forces usually depend inversely on the distance between the particles. This expression is accessed using <name>.r, where <name> is the physics interface node name. So, if the name is pt, then this variable is accessed using pt.r.

As an example, the gravitational force on particle i depends on the position vector and mass of all other particles:

where ri is the position vector of the ith particle, G is the gravitational constant, and m is the mass. To enter this as a user-defined force, enter (in 2D):

where tol is a user-defined parameter to prevent divide by zero for the ith particle. In practice it is quite difficult to choose the value of tol. It should in general be a small fraction of the smallest distance you want to allow between particles.

When reading or writing the expressions for a user-defined particle-particle interaction force, the dest() operator is used to identify properties of the particle that is being subjected to a force, while the omission of the dest() operator indicates some property of a particle that is exerting the force. For example, when computing the force on the ith particle, the expression qx-dest(qx) is the difference between the x-coordinate of some other particle (say, the jth particle) and the x-coordinate of the ith particle.

The fact that all particles can interact with all other particles in the system means that a full Jacobian matrix is generated at each time step when solving. Assembly and factorization of such a matrix is very expensive in both time and memory.

By default, the check box is selected. This means the contribution to the Jacobian matrix is ignored due to the particle-particle interaction force. This also means that the problem solves much faster and requires much less memory. The drawback of this is that the Jacobian is not exact, and the solver therefore needs to take very small time steps when solving.

	Rotating Galaxy: Application Library path Particle_Tracing_Module/Tutorials/rotating_galaxy

By default, the check box is cleared. If this check box is selected, enter a value or expression for the rc (SI unit: m). The default is 5 mm. If the distance between particles is greater than the cutoff length, the particle-particle interaction force between them is set to zero.