Erosion Theory
The Erosion feature calculates the rate of erosive wear or the total mass removed per unit area due to the impact of particles on a surface. It includes the following models:
Finnie
Finnie (Ref. 28) defined the volume removed from a surface as:
The parameters are defined as follows:
•
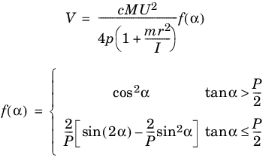
c (dimensionless) is the fraction of particles cutting in an idealized manner.
•
M (SI unit: kg) is the total mass of eroding particles.
•
U (SI unit: m/s) is the magnitude of the incident particle velocity.
•
p (SI unit: Pa) is the Vickers hardness of the material.
•
m (SI unit: kg) is the mass of an individual particle hitting the surface.
•
r (SI unit: m) is the average particle radius.
•
I (SI unit: kg·m2) is the moment of inertia of an individual particle about its center of mass. For an isotropic sphere, I = 2mr2/5.
•
α (SI unit: rad) is the angle of incidence, with α = 0 tangent to the surface and α = π/2 normal to the surface.
•
P is a dimensionless parameter, defined as P = K/(1+mr2/I), where K (dimensionless) is the ratio of vertical and horizontal forces acting on the particle.
In the Finnie model, particles are assumed to remove mass from the surface via an idealized cutting mechanism. It does not predict any erosive wear by particles at normal incidence to a surface, and is recommended for modeling erosion of ductile materials by particles at small angles of incidence.
E/CRC
The E/CRC model defines the erosion rate in terms of the ratio of mass lost by the surface to mass of incident particles:
where C is an erosion model coefficient, Fs is the particle shape coefficient, and BH is the Brinell hardness of the wall material (all dimensionless). The angle of incidence α is measured in radians.
Oka
The Oka model defines the volume of surface material removed per unit mass of incident particles (in units of mm3/kg) as:
where E(α) is the etch rate, E90 is the etch rate at normal incidence, and g(α) is an angular dependence function:
where v’ is the reference velocity; D’ is the reference diameter; the dimensionless parameters n1, n2, and k2 are defined as
and the remaining dimensionless parameters s1, s2, q1, q2, K, k1, and k3 are constants.
DNV
The DNV model defines the erosion rate in terms of the ratio of mass lost by the surface to mass of incident particles:
where K and n are dimensionless constants that depend on the surface material.