If the particles are very small or the gas is extremely rarefied, consider selecting the Include rarefaction effects check box in the settings for the Particle Tracing for Fluid Flow interface to include some of the corrections described in this section.
where dp (SI unit: m) is the particle diameter and
λ (SI unit: m) is the mean free path of molecules in the surrounding fluid.
(5-6)
|
•
|
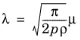
p (SI unit: Pa) is the gas pressure,
|
|
•
|
ρ (SI unit: kg/m 3) is the gas density, and
|
|
•
|
μ is the gas dynamic viscosity (SI unit: Pa·s).
|
This is very similar to the expression given in Ref. 6, albeit with a slight simplification. Jennings (
Ref. 6) defines the mean free path as
(5-7)
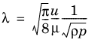
Comparing Equation 5-6 to
Equation 5-7, it is clear that the COMSOL implementation uses
u = 0.5. Jennings instead suggests
u = 0.4987445. Allen and Raabe (
Ref. 7) suggest
u = 0.498 when treating the molecules as hard elastic spheres. You can multiply the mean free path by a user-defined coefficient by selecting
User-defined correction from the
Mean free path calculation list in the settings for the
Drag Force node.
The definition of the slip correction factor S is given for each available rarefaction model in
Table 5-1 below. In the expressions for the
Basset,
Epstein, and
Phillips models, the factor
2Kn is explicitly given as a reminder that these models were originally defined for a Knudsen number in terms of particle radius, not diameter. Additional details about each model are given in the ensuing subsections.
The Cunningham-Millikan-Davies model, or CMD model, uses three dimensionless, user-defined coefficients to define the correction factor:
The default values of the three coefficients are C1 =
2.514,
C2 =
0.8, and
C3 =
0.55. Allen and Raabe (
Ref. 7) list the coefficients given by various authors.
Note that in some references (7,
9), the Knudsen number is defined by using the particle radius as the characteristic length scale, not the diameter. When importing coefficients from such a reference, multiply the coefficients
C1 and
C2 by 2, and divide the coefficient
C3 by 2.
For example, Millikan (Ref. 9) suggested values of 0.864, 0.290, and 1.25. To use Millikan’s fitting parameters in COMSOL, you should instead enter the values
1.728,
0.580, and
0.625. Even with this adjustment, the fitting parameters used by Millikan differ significantly from those used by more recent authors (
Ref. 7) in part because Millikan used a different coefficient to compute the mean free path of air.
Epstein (Ref. 10) analytically derived the net force on a spherical particle in a rarefied gas in the limit of extremely high Knudsen number, so that the mean free path of molecules is much greater than the particle diameter:
(5-8)
|
•
|
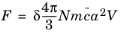
N (SI unit: 1/m 3) is the number density of molecules in the gas,
|
|
•
|
m (SI unit: kg) is the molecular mass of the gas,
|
|
•
|
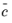 (SI unit: m/s) is the average speed of the molecules in the gas, |
|
•
|
a (SI unit: m) is the particle radius, and
|
|
•
|
V (SI unit: m/s) is the norm of the average velocity of the gas relative to the particle.
|
The dimensionless parameter δ has different values depending on the type of reflection the gas molecules experience on the particle surface. For specular reflection,
δ = 1.
For diffuse reflection, δ = 1 + π/8. The particle is assumed to be a perfect thermal conductor. Furthermore, this type of diffuse reflection is called “diffuse reflection with accommodation”, meaning that the reflected particle velocity is sampled from a Maxwell distribution based on the effective temperature of the particle. That is, both the reflected particle speed and direction are sampled randomly.
(5-9)
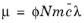
where λ is the mean free path of molecules and
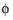
is a dimensionless coefficient. Epstein and Millikan (Refs.
8,
9, and
10) used
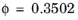
, while subsequent authors (Refs.
6 and
7) used values of approximately
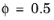
. Using the more up-to-date value and substituting
Equation 5-9 into
Equation 5-8 yields
Let σ (dimensionless) be the fraction of molecules that undergo diffuse reflection with accommodation at the particle surface, while the remainder undergo specular reflection. Many authors (Refs.
7,
8,
9, and
10) report values of approximately
σ = 0.9. Then
The Basset model is a first-order correction for relatively small Knudsen numbers; that is, terms of order
λ/a are retained whereas terms of order (
λ/a)
2 and higher are neglected. Under this assumption, Epstein (
Ref. 10) provides a simplified version of Basset’s formula for drag force with a nonzero slip factor,
(5-10)
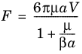
The numerator is simply the expression for Stokes drag in a continuum flow. In the denominator, a (SI unit: m) is the particle radius, and the radio
μ/β (dimensionless) is the slip factor, given as
(5-11)
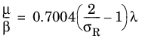
where, similar to the Epstein model,
σR is the fraction of gas molecules that undergo diffuse reflection with accommodation, and the remaining fraction are assumed to undergo specular reflection.
Substituting Equation 5-11 into
Equation 5-10, and noting that
λ/a = 2Kn, yields
Finally, in Ref. 10 Epstein used a coefficient of
0.3502 when defining the mean free path, whereas in the COMSOL implementation this coefficient is
0.5, nearly equal to values given in more recent publications (Refs.
6 and
7). To compensate for this change, the factor of
0.7004 may be set to unity in the previous equation, yielding the equation for the slip correction factor implemented in COMSOL:
in which terms of order x2 can be dropped for
x much smaller than unity.
If the Phillips model (
Ref. 11) is used, the correction factor is defined as:
where c1 and
c2 (dimensionless) are functions of the accommodation coefficient:
, the surrounding fluid may be treated as a continuum flow; a correction factor is not necessary. However, if the Knudsen number is significantly greater than zero, rarefaction effects should be taken into account. In that case, select the Include rarefaction effects check box in the physics interface Particle Release and Propagation section. The drag force CD (dimensionless) is then defined as the drag force for continuum flow CD,C (dimensionless), divided by a slip correction factor S (dimensionless):
