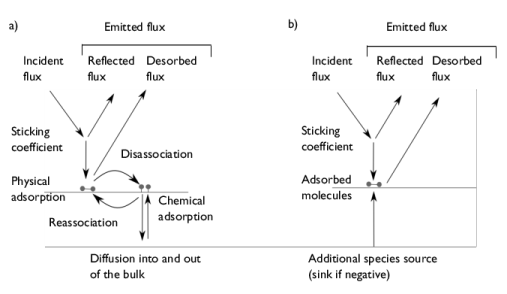
There is considerable complexity in the detailed physics of gas adsorption and desorption (see Ref. 2). Some of this complexity is summarized in Figure 3-4a, which shows some of the processes involved in the adsorption and desorption of an imaginary diatomic molecule. Molecules incident on a wall of the vacuum system are either reflected or adsorbed. The sticking coefficient defines the probability that an incident molecule is adsorbed. The molecule is usually physically adsorbed initially, being bound to the surface by weak van der Waals interactions between the adsorbate and the atoms in the solid surface, or in the case of multiple physically adsorbed layers, between the adsorbate and the underlying layer of adsorbed molecules. Molecules adjacent to the surface can then dissociate and chemically adsorb on the metal surface of the chamber. The reverse processes: chemical desorption, followed by reassociation can increase the number of physically adsorbed molecules on the surface. These physically adsorbed molecules can dissociate from the surface and consequently contribute to the desorbed flux. In addition to these processes, gases can pass through the walls of a vacuum system by the process of diffusion. Depending on the method of manufacturing, a newly constructed vacuum system contains a certain amount of dissolved gas in its walls. Initially the concentration profile of the gases is probably uniform through the thickness of the wall. When the chamber is pumped out, over a long period of time this uniform concentration changes to a roughly linear profile with a high concentration on the outside and a low concentration on the inside. It takes some time for this concentration profile to develop and the process of reaching this point is frequently referred to as diffusion in the vacuum literature. Once an equilibrium profile is reached then a constant mass transport occurs along the concentration gradient. This is known as permeation (although the process itself is, of course, diffusive). Permeation needs to account for the adsorption of the molecules onto the exterior surfaces of the vacuum chamber and the desorption of the molecules from the interior of the chamber.

Modeling the adsorption and desorption of molecules on the surface of a vacuum chamber at this level of detail is possible if the Free Molecular Flow interface is coupled with the Chemical Reaction Engineering Module’s Surface Reactions interface. However, in practice there is usually insufficient data available to fully characterize the reactions occurring on the surfaces of the chamber. Furthermore, the barriers to desorption of physically adsorbed species are small at room temperature, so physical adsorption has little effect on molecular transport in the vacuum system (Ref. 3). It is therefore usually appropriate to consider only chemical adsorption. Given these considerations, the Adsorption/Desorption feature considers only the chemical adsorption of the molecule as a whole (see Figure 3-4b). If the molecule dissociates on adsorption then it is still possible to use this mechanism for practical modeling, but allowance must be made for the fact that the boundary condition tracks the total number of moles of the original gas molecule that have been adsorbed (in the example of the diatomic molecule the number of moles of the adsorbed species is double this number). An additional source term for the number of adsorbed molecules can be used to include the effects of diffusion and permeation through the chamber walls. Very complex and realistic situations can be modeled with this approach.

where J is the emitted molecular flux (SI unit: molecules/m2/s), S is the sticking coefficient, G is the incident molecular flux (SI unit: molecules/m2/s), NA is Avagadro’s number, nads is the number of adsorbed moles (SI unit: mol/m2), D is the desorption rate (SI unit: mol/m2/s), and Γ is the additional source term for the adsorbed molecules (SI unit: mol/m2/s). S, D, and Γ, along with an initial value for the number of adsorbed molecules (nads,0), are specified in the boundary condition. These values can be specified as arbitrary functions of the concentration of adsorbed species (fmf.n_ads) allowing for highly flexible modeling of the adsorption and desorption process.