The flux of molecules from x′ arriving at point x as shown in Figure 3-2 is derived.

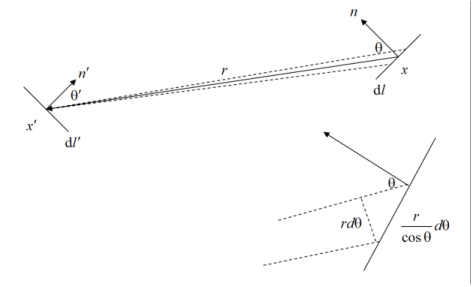
Let the total rate of emission of molecules per unit area at x′ be J′ (SI unit: 1/(m2·s)). In the steady state J′ is independent of time. Note that in practice, the molecules take a finite time to travel from x′ to x, but this is not accounted for in the calculations (which are consequently quasi-static).

In 2D the flux of molecules with speeds between c′ and c′ + dc′ leaving x′ with angles between θ′ and θ′ + dθ′ is

In 3D the flux of molecules with speeds between c′ and c′ + dc′ leaving x′ with angles between θ′ and θ′ + dθ′ and ′ and ′ + d′ is

In 2D, molecules leaving x′ at angles between θ′ and θ′ + dθ′ is spread over an area of rdθ′ in the plane with normal parallel to r at x. This plane is in turn projected onto an area

on the surface at x (see Figure 3-2). In 3D, molecules leaving x′ at angles between θ′ and θ′ + dθ′ and 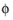′ an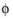d ′ + d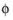′ is spread over an area of

in the plane with normal parallel to r at x giving a projected area of

The arriving flux per unit area at x from x′, dG (m−2s−1), is therefore:

where the integral is over the path l′, or the surface S′ that includes all the surfaces in the line of sight of x.

By the definition of the probability distribution, both the integrals over c′ evaluate to 1. Substituting for ρ(θ′) the following equations are left:

In the Free Molecular Flow interface, COMSOL Multiphysics computes the incident flux on the surfaces G as the dependent variable. The outgoing flux from a surface (usually specified in terms of G by the boundary condition) is also available as fmf.J.