Small Concert Hall Acoustics

Designing structures and open spaces with respect to sound quality is important for concert halls, outdoor environments, and even the rooms of a house. Simulating acoustics in the high-frequency limit, where the wavelength is smaller than the geometrical features, is best done with ray acoustics.

This tutorial model shows the basic steps and principles used when setting up a model using the Ray Acoustics physics interface. In the model, the acoustics of a small concert hall is analyzed. The model setup includes an omnidirectional sound source, wall boundary conditions for specular and diffuse scattering, sound pressure evaluation, a receiver data set used to reconstruct a temporal impulse response plot, and an energy response (reflectogram). The results are compared to simple reverberation time estimates.

Model Definition

In this model the acoustics of a generic “small concert hall” are analyzed. The model is that of a listening environment with a volume of 460 m3 and a total surface area of 390 m2. The listening environment is fitted with absorbers and diffusers; their location is not particularly optimized and does probably not follow design rules. The aim of this tutorial is to describe the important modeling steps to perform a room acoustics simulation using ray tracing. The geometry of the concert hall is depicted in Figure 1.

Figure 1: Geometry of the small concert hall.

An omni-directional source is located at the coordinates (xs, ys, zs) near the stage. The receiver (microphone) is located at the coordinates (xr, yr, zr). These are parameters found under . The location of the receiver can be changed in postprocessing while the location of the source needs to be changed before running the model.

The absorption properties if the various surfaces (windows, seats, diffusers, floor, entrance, walls, and absorbers) are generic values taken from Ref. 1 and 2. The data is given in octave band values and imported from the file small_concert_hall_absorption_parameters.txt file into an interpolation function (lookup table). Moreover, the (intensity) attenuation of air is imported from the file small_concert_hall_volume_absorption.txt. Note that when the (volume) attenuation coefficient m (loaded from the file) is entered in the section it is the amplitude attenuation αext (= 0.5·m) that should be used. The difference is a factor 0.5.

Results and Discussion

The local wavefront sound pressure level (SPL) is depicted in Figure 2 after 10 ms and in Figure 3 after 20 ms propagation. When the compute intensity option is selected in the Ray Acoustics interface, wavefront curvature, intensity, and SPL is calculated along each ray. They allow visualization of the local acoustic properties. However, it is the acoustic power transported by each ray that is important when calculating the impulse response (IR) and when visualizing the sound pressure level at surfaces. This means that the compute power option should always be selected for IR computation but the compute intensity can be turned off. Only selecting will also make the model run slightly faster and reduce the number of degrees of freedom (DOFs) solved for.

The temporal IR for the default source location configuration used in the model is depicted in Figure 4 and the frequency domain (FFT) of the IR is depicted in Figure 5. For most practical application and further postprocessing the impulse response should be exported under the node by adding a export. Per default the IR has a sampling frequency of 44100 Hz.

When an IR is reconstructed from a ray tracing simulation, information is inferred and put back into the time signal. The quality of the simulated IR increases with the number of rays (this model uses 10000) as well as the frequency resolution of the absorption, scattering, and source data (this data can be difficult to get from vendors but can often be simulated). In this model, octave band resolution is used. The Impulse Response plot also allows the use of 1/3 octave and 1/6 octave frequency resolution.

Figure 2: Ray location and SPL after 10 ms.

Figure 3: Ray location and field SPL after 20 ms.

Figure 4: Temporal impulse response reconstructed from the ray data at the receiver location.

Figure 5: FFT of the impulse response (no smoothing/windowing is used).

Figure 6: SPL in a cross section 60 cm above the ground at the location of the audience.

The sound pressure level in a cross section located above the seating section is depicted in Figure 6. It is calculated using the feature, available as a sub-node to all wall conditions. In this case it is added to a transparent surface ( used as ). The feature can be added to all other walls to postprocess the SPL distribution there if necessary.

In ray tracing methods, the intensity I and RMS pressure prms of the n’th ray detected by the receiver sphere is expressed as

where Vr is the receiver volume, Lr is the distance traveled by the ray inside the receiver, and Qn is the power carried by the ray (see, for example, Ref. 3). The intensity is evaluated using the expression re1dist*rac.Q/re1vol. Plotting this information in a Ray plot as function of the arrival time yields the (discrete time) energy impulse response. It is also sometimes known as a reflectogram. It is plotted for the 500 Hz and the 16 kHz octave bands in Figure 7. The slope of the curves (point data) is related to the reverberation time of the room. The slope is usually assessed using, for example, Shroeder’s backward integration or a moving integration/averaging. This is not done here but can be done in an external tool if the data is exported. In Figure 7 approximate trend lines have been added; their slope (60 dB down which is 6 decades for log10(In)) predict the T60 reverberation time. The values can be compared to the predicted values shown in Figure 8. The graph shows the values both with and without the effect of air attenuation. The values are calculated using the Sabine equation used in statistical room acoustics

where V is the room volume, S is the total surface area, m is the volume attenuation, and

is the average wall absorption (see Ref. 2). For the two frequency bands the results from Figure 7 show good agreement with the results in Figure 8.

Figure 7: The raw data of the energetic impulse response or reflectogram. The slope represents the reverberation time in the given octave band.

Figure 8: Reverberation time estimates based on the Sabine formula. The curve with and without the volume absorption of air. The importance of including air absorption is evident at the higher frequencies.

Notes About the COMSOL Implementation

Results

There are several options that can be selected on the node that are useful when working with ray acoustic models and especially when evaluating the impulse response.

•

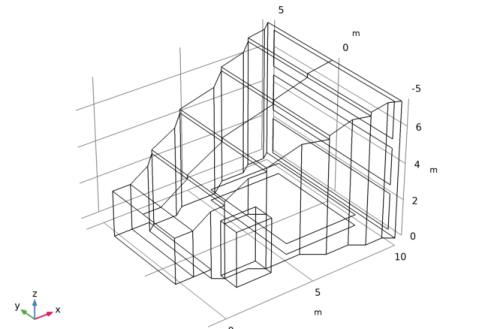
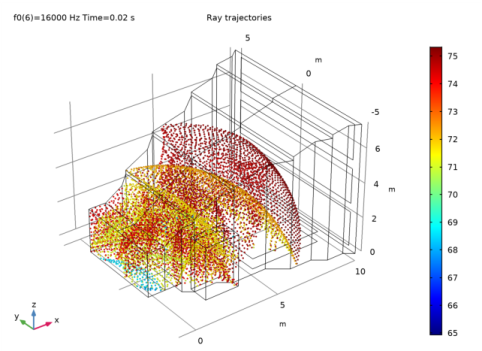
When first setting up plots, it is useful to select the option as some plots take a long time to render. Another trick is to use only a few rays initially.

•

Once the plots are set up, then before running the model (with a large number of rays), select the option. Once the model has solved the plots will be rendered. This is very useful when running the model over lunch break or over night since rendering the IR plot often takes longer time than solving the model.

•

Before saving the model, remember to set the list to . Then all plots do not need to be re-rendered once the model is opened again.

Extra Time-Steps Convergence Analysis

When this tutorial model is solved the solution is only stored every 0.1 s. This reduces the file size when saving. For postprocessing it is typically necessary with a much finer time resolution. Ideally there should be one time before and after each ray-wall interaction and one time before and after a ray crosses the receiver. This is achieved using the in the Receiver data set. To find an adequate value a small convergence test can be run. This is done in the model (see the last plot also shown in Figure 9). For a single band, plot the power rac.Q detected at the receiver using a Ray plot; do this while increasing the number of extra time steps. In this model the is increased. Once the solution does not change any more, enough extra times have been used. In Figure 9 you can see that the red dots are on top of all the cyan circles (except a few). This means that a proportionality factor of 30 is an adequate choice for all the postprocessing.

Figure 9: Graph used to evaluate how many extra time steps (time steps added in-between the stored times) that are needed when reconstructing the impulse response in order to get consistent results.

References

1. M. Vorländer, Auralization, Fundamentals of Acoustics, Modeling, Simulation, Algorithms and Acoustic Virtual Reality, Springer, 2008.

2. H. Kuttruff, Room Acoustics, CRC Press, 2009.

3. Z. Xiangyang, C. Ke'an, and S. Jincai, “On the accuracy of the ray-tracing algorithms based on various sound receiver models,” Appl. Acoust., vol. 64, pp. 433-441, 2003.

Acoustics_Module/Building_and_Room_Acoustics/small_concert_hall

Modeling Instructions

This section contains the modeling instructions for the Absorptive Muffler model. They are followed by the Geometry Sequence Instructions section.

From the menu, choose .

New

In the window, click .

Model Wizard

In the window, click .

In the tree, select .

Click .

In the tree, select .

Click .

The geometry is set up by importing a geometry sequence. The sequence imports the small concert hall geometry and sets up several selections. The predefined selections simplify the rest of the model setup.

Geometry 1

In the toolbar, click .

Browse to the model’s Application Libraries folder and double-click the file small_concert_hall_geom_sequence.mph.

In the toolbar, click .

Click the button in the toolbar.

Import the model parameters form a file. The parameters include the band center frequency f0, the location of the source and receiver, as well as the room volume.

Global Definitions

Parameters 1

In the window, under click .

In the window for , locate the section.

Click .

Browse to the model’s Application Libraries folder and double-click the file small_concert_hall_parameters.txt.

Proceed and set up interpolation functions for the absorption coefficients of the different surfaces in the concert hall. The data is easily stored in one .txt file. Also define an interpolation function for the intensity attenuation of air (given at 50 % relative humidity and 20 deg. C).

Interpolation 1 (int1)

In the toolbar, click and choose .

In the window for , locate the section.

From the list, choose .

Click .

Browse to the model’s Application Libraries folder and double-click the file small_concert_hall_absorption_parameters.txt.

In the text field, type 1.

Click .

Find the subsection. In the table, enter the following settings:


Function name	Position in file
a_walls	1
a_entrance	2
a_windows	3
a_floor	4
a_diffuser	5
a_seats	6
a_absorbers	7

Locate the section. From the list, choose .

Locate the section. In the text field, type Hz.

In the text field, type 1.

Interpolation 2 (int2)

In the toolbar, click and choose .

In the window for , locate the section.

From the list, choose .

Click .

Browse to the model’s Application Libraries folder and double-click the file small_concert_hall_volume_absorption.txt.

Click .

In the text field, type m_air.

Locate the section. From the list, choose .

Locate the section. In the text field, type Hz.

In the text field, type 1/m.

Now import the variables that define the reverberation time (T60) based on the simple Sabine equations. This also requires setting up integration operators for all the surfaces.

Definitions

Variables 1

In the window, expand the node.

Right-click and choose .

In the window for , type Variables: Reverberation Time Estimates in the text field.

Locate the section. Click .

Browse to the model’s Application Libraries folder and double-click the file small_concert_hall_variables.txt.

Integration 1 (intop1)

In the toolbar, click and choose .

In the window for , type intop_windows in the text field.

Locate the section. From the list, choose .

From the list, choose .

Integration 2 (intop2)

In the toolbar, click and choose .

In the window for , type intop_seats in the text field.

Locate the section. From the list, choose .

From the list, choose .

Integration 3 (intop3)

In the toolbar, click and choose .

In the window for , type intop_diffusers in the text field.

Locate the section. From the list, choose .

From the list, choose .

Integration 4 (intop4)

In the toolbar, click and choose .

In the window for , type intop_floor in the text field.

Locate the section. From the list, choose .

From the list, choose .

Integration 5 (intop5)

In the toolbar, click and choose .

In the window for , type intop_entrance in the text field.

Locate the section. From the list, choose .

From the list, choose .

Integration 6 (intop6)

In the toolbar, click and choose .

In the window for , type intop_walls in the text field.

Locate the section. From the list, choose .

From the list, choose .

Integration 7 (intop7)

In the toolbar, click and choose .

In the window for , type intop_absorbers in the text field.

Locate the section. From the list, choose .

From the list, choose .

Now it is time to set up and define the physics and boundary conditions of the model. To compute the impulse response, it is necessary to model the intensity and power along the rays. The model only uses a surface mesh. Propagation in the unmeshed domains requires the definition of material properties at the interface level (in the section ). Also set up boundary conditions for the different walls (boundaries).

Ray Acoustics (rac)

In the window, click .

In the window for , locate the section.

From the list, choose .

Locate the section. In the cext text field, type c0.

In the ρext text field, type rho0.

In the αext text field, type 0.5*m_air(f0).

Multiplication by 0.5 is necessary as the input in COMSOL is defined for the amplitude attenuation and not the intensity attenuation (as given in the interpolation data).

Ray Properties 1

In the window, under click .

In the window for , locate the section.

In the f text field, type f0.

Wall 2

In the toolbar, click and choose .

In the window for , type Wall: Walls in the text field.

Locate the section. From the list, choose .

Locate the section. In the α text field, type a_walls(f0).

Wall 3

In the toolbar, click and choose .

In the window for , type Wall: Entrance in the text field.

Locate the section. From the list, choose .

Locate the section. In the α text field, type a_entrance(f0).

Wall 4

In the toolbar, click and choose .

In the window for , type Wall: Windows in the text field.

Locate the section. From the list, choose .

Locate the section. In the α text field, type a_windows(f0).

Wall 5

In the toolbar, click and choose .

In the window for , type Wall: Floor in the text field.

Locate the section. From the list, choose .

Locate the section. In the α text field, type a_floor(f0).

Wall 6

In the toolbar, click and choose .

In the window for , type Wall: Diffusers in the text field.

Locate the section. From the list, choose .

In the γs text field, type 1-s_diffuser.

Locate the section. In the αs text field, type a_diffuser(f0).

In the αd text field, type a_diffuser(f0).

In this model the scattering coefficient s_diffuser is constant across the frequency bands. It can of course also be defined as an interpolation function.

Wall 7

In the toolbar, click and choose .

In the window for , type Wall: Seats in the text field.

Locate the section. From the list, choose .

Locate the section. In the α text field, type a_seats(f0).

Wall 8

In the toolbar, click and choose .

In the window for , type Wall: Absorbers in the text field.

Locate the section. From the list, choose .

Locate the section. In the α text field, type a_absorbers(f0).

Wall 9

In the toolbar, click and choose .

In the window for , type Wall: SPL cross section in the text field.

Locate the section. From the list, choose .

The option is used here as this surface only is meant for visualizing the SPL in a cross section. Use rendering to select the surface that is located inside the concert hall.

Click the button in the toolbar.

Select Boundary 40 only.

Sound Pressure Level Calculation 1

In the toolbar, click and choose .

Release from Grid 1

In the toolbar, click and choose .

In the window for , locate the section.

In the qx, 0 text field, type x_s.

In the qy, 0 text field, type y_s.

In the qz, 0 text field, type z_s.

Locate the section. From the list, choose .

In the Nw text field, type Nrays.

Locate the section. In the Psrc text field, type P0.

Ray Termination 1

In the toolbar, click and choose .

In the window for , locate the section.

From the list, choose .

In the Ith text field, type 1e-13[W/m^2].

Mesh 1

Free Triangular 1

In the window, under right-click and choose .

In the window for , locate the section.

From the list, choose .

Size

In the window, click .

In the window for , locate the section.

From the list, choose .

Click .

Proceed and solve the model by adding a parametric sweep over the center frequency variable f0. This represents the center frequency of the octave bands analyzed in this model, in order to get a broadband response. The first time you set up and solve the model it can be useful to reduce the number of rays by changing the value of the parameter Nrays to, for example, 1000. This will make postprocessing faster. Remember that the quality of the results in acoustic ray tracing increase for an increasing number of rays and more narrow frequency bands (you need to have wall absorption data with the desired resolution). In the Ray Acoustics interface the impulse response plot can handle octave, 1/3 octave, and 1/6 octave data.

Study 1

Step 1: Ray Tracing

In the window, expand the node, then click .

In the window for , locate the section.

From the list, choose .

In the text field, type 0 0.01 0.02 range(0.1,0.1,1.4).

The times entered here represent instances where the solution is stored (the model size on disc depends in part on this). Much smaller time steps are used internally by the solver. In postprocessing when reconstructing the impulse response additional time steps are rendered and used by the data sets.

Parametric Sweep

In the toolbar, click .

Using the parametric sweep is important as this gives the frequency resolution (here in full octaves). The ray propagation model is solved once per frequency band. The data is collected in postprocessing, by the receiver data set and the impulse response plot, to generate the broadband response.

In the window for , locate the section.

Click .

In the dialog box, choose from the list.

In the text field, type 500.

In the text field, type 20000.

Click .

Solving the model takes a couple of minutes and uses less than 2 GB of RAM (depending on your hardware). This will increase for an increasing number of rays.

In the toolbar, click .

Results

Ray Trajectories (rac)

In the window for , locate the section.

From the list, choose .

In the toolbar, click .

Ray Trajectories 1

In the window, expand the node, then click .

In the window for , locate the section.

Find the subsection. From the list, choose .

Color Expression 1

In the window, expand the node, then click .

In the window for , locate the section.

In the text field, type rac.Lp.

In the toolbar, click .

This should reproduce the image in Figure 2.

Ray Trajectories (rac)

In the window, click .

In the window for , locate the section.

From the list, choose .

In the toolbar, click .

This should reproduce the image in Figure 3.

On the node you have several options that are useful when postprocessing ray tracing simulations, where rendering plots can be time consuming. This is especially true for the impulse response plots. While setting up plots, it is useful to select such that the plots are not generated every time you change an option. It is also good practice to save the plots in the model such that they are already rendered when you open your model at a later stage. Finally, once you have set up all the plots and you are ready to run the model again, it can be useful to enable . All plots will then be recomputed after the model is solved, for example, running over night.

In the window, click .

In the window for , locate the section.

Select the check box.

Locate the section. From the list, choose .

Now set up all the data sets you will need for postprocessing the results. First, set up the receiver data set that includes all the solved frequency bands (for a broadband analysis). Then, set up a receiver for the first and for the last frequency band. Finally, set up a series of data sets that will be used in a convergence analysis performed later on. The latter is optional, but it shows how the value is chosen and set equal to 30 in all the receiver data sets used.

Receiver 3D 1

In the toolbar, click and choose .

In the window for , type Receiver 3D - All Bands in the text field.

Locate the section. Find the subsection. In the text field, type x_r.

In the text field, type y_r.

In the text field, type z_r.

Find the subsection. In the text field, type Nrays.

In the text field, type Vol.

In the text field, type dsr.

Locate the section. From the list, choose .

In the text field, type 30.

Receiver 3D - All Bands 1

Right-click and choose .

In the window for , type Receiver 3D - 500 Hz Band in the text field.

Locate the section. From the list, choose .

In the list, select .

Receiver 3D - 500 Hz Band 1

Right-click and choose .

In the window for , type Receiver 3D - 16k Hz Band in the text field.

Locate the section. In the list, select .

Group 1

In the window, right-click and choose .

In the window for , type Group: Convergence Analysis Data Sets in the text field.

Receiver 3D 4

In the toolbar, click and choose .

In the window for , type Receiver 3D - Single Band (prop = 1) in the text field.

Locate the section. From the list, choose .

Locate the section. Find the subsection. In the text field, type x_r.

In the text field, type y_r.

In the text field, type z_r.

Find the subsection. In the text field, type Nrays.

In the text field, type Vol.

In the text field, type dsr.

Locate the section. From the list, choose .

Receiver 3D - Single Band (prop = 1) 1

Right-click and choose .

In the window for , type Receiver 3D - Single Band (prop = 10) in the text field.

Locate the section. In the text field, type 10.

Receiver 3D - Single Band (prop = 10) 1

Right-click and choose .

In the window for , type Receiver 3D - Single Band (prop = 30) in the text field.

Locate the section. In the text field, type 30.

Receiver 3D - Single Band (prop = 30) 1

Right-click and choose .

In the window for , type Receiver 3D - Single Band (prop = 100) in the text field.

Locate the section. In the text field, type 100.

1D Plot Group 2

In the toolbar, click .

In the window for , type Impulse Response in the text field.

Locate the section. From the list, choose .

Impulse Response 1

In the toolbar, click and choose .

Rendering the impulse response will typically take longer time than solving the model (up to 20-30 min for this plot alone). The plot is not just a representation of computed data but consists of a reconstruction (computation) of a signal based on the ray data picked up at the receiver.

Click .

This should reproduce the impulse response shown in Figure 4. The impulse response is the most important result of this model. The signal can be exported under the node and used for further analysis in an external signal processing tool. The response is reconstructed from the ray data detected by the data set (arrival time, power, and band center frequency). It has a default sampling frequency of 44100 Hz. This can be changed under the section in the plot settings window.

Impulse Response 1