PDF
Acoustic Reflections off a Water-Sediment Interface
Introduction
This validation model computes the reflection coefficient of acoustic waves off a water-sediment interface. Homogeneous waves are incident from a fluid (water) domain and are reflected and transmitted at a water-sediment interface. The sediment domain is modeled using Biot’s theory with the use of the Poroelastic Waves interface. It includes the detailed interaction between the pressure waves in the saturating fluid and the elastic waves in the porous matrix (the sediment). The model results are compared with those obtained by Stoll and Kan (Ref. 1). A visual comparison of the results with those presented in Ref. 1 shows good agreement.
Figure 1: Sketch of the water-sediment system. The computational unit cell has the width W and the height H with perfectly matched layers at the top and bottom. λ is the acoustic wavelength in water. An acoustic wave with wave vector k is incident at an angle θ0 on the water-sediment interface.
Knowledge about the plane wave reflection and refraction coefficients are important when interpreting acoustic data taken from marine seismology. The kind of model studied here can provide insight into the different phenomena at play. The sediment is modeled using Biot’s theory with the addition of the porous matrix skeleton having viscoelastic properties. This is achieved by simply allowing the bulk modulus and the shear modulus to have a small imaginary component (a constant attenuation factor). Inside the porous material, three types of waves can propagate: a fast and a slow pressure wave, and a shear wave. The interplay between these waves and the incoming homogeneous pressure wave in the fluid results in nontrivial behavior of the reflection coefficient. See Ref. 1 for further discussion.
Model Definition
A sketch of the modeled system is shown in Figure 1. An acoustic wave is incident on the water-sediment interface at an angle θ0, defining the wave vector
where ω is the angular frequency 2πf. The wave vector is used to define an incident plane wave of the form
where x = (x, y). The incident wave and wave vector are defined as variables in the model.
The fluid domain is modeled by classical pressure acoustics (lossless) solving the Helmholtz equation. The sediment domain is modeled by Biot’s theory solving for both the pressure and the displacement field of the porous matrix. The coupled multiphysics problem is set up using the Acoustic-Poroelastic Waves Interaction multiphysics interface.
The problem is 2D and is modeled as a periodic structure using Floquet periodic conditions on both the acoustic and the porous domains. To ensure that the problem is well defined numerically, the domain size is set to depend on the wavelength in water (thus the frequency). The width of the computational unit cell W is equal to the wavelength and the height H is equal to two times the wavelength. The computational domain is truncated, in both the fluid and in the porous domain, using perfectly matched layers (PMLs). The thickness is set equal to one third of the wavelength.
The material parameters necessary for defining the properties of the porous domain are taken from Ref. 1 and some are calculated using these values. The porous material is here assumed to be sand. The most important parameters and their definitions are given in Table 1 below.
Table 1: Porous Material Parameters for Sand.
Symbol
Value
Description
 µF
1·10-3 Pa·s
Fluid viscosity (water)
 ρF
1000 kg/m3
Fluid density (water)
 εP
0.47
Porosity
 κP
1·10-6 cm2
Permeability
 Kb
4.36·107 Pa
Bulk modulus of frame (drained porous matrix)
 Ks
3.6·1010 Pa
Bulk modulus of solid grains (constituting the frame)
 αB
1−Kb/Ks = 0.999
Biot-Willis coefficient: Because it is very close to 1 the frame is said to be limp.
 logdec
0.15
Logarithmic decrement factor
 Kbc
(1+i·logdec/π)·Kb
Complex bulk modulus of frame
 G
2.61·107 Pa
Shear modulus of frame (drained porous matrix)
 Gc
(1+i·logdec/π)·G
Complex shear modulus of frame
 ρs
2650 kg/m3
Solid density (of material constituting the frame)
 ρd
(1-εP)·ρs
= 1404.5 kg/m3
Drained density (of the porous matrix)
 τ
1.25
Tortuosity (chosen, not specified in Ref. 1)
 a
4·10-3 cm
Pore size parameter (chosen to have fc = 100 Hz)
 fr
µF/(2π·ρF·a2)
= 99.5 Hz
Reference frequency: frequency at which the viscous boundary layer thickness (viscous penetration depth) is equal to the pore size parameter a. This value is automatically calculated by COMSOL
Note: Further information about the physics solved by the Poroelastic Waves interface, about Biot’s theory, and about the meaning of the material parameters is given in the documentation. Press Ctrl+F1 and browse to the Acoustics Module and the User’s Guide. Theory is found in Elastic Waves Interfaces > Theory for the Poroelastic Waves Interfaces.
Results and Discussion
The reflection coefficient R and the absorption coefficient α are plotted for different combinations of the angle of incidence and the frequency (the model parameters). The reflection coefficient is the complex ratio of the reflected to the incident waves (at the interface) and is given by
where the subscript sc stands for scattered and tot for total. The absorption coefficient gives a measure of the relative absorbed energy and is given by
The absolute value of the reflection coefficient R is shown in Figure 2 and Figure 3. Note that average of the reflection coefficient across the interface is used. This is because the model extracts the effective homogenized properties of the water-sediment interface. In the first figure, R is depicted as function of the angle of incidence θ0 and in the second figure as function of the frequency f. The absorption coefficient α, corresponding to the reflection coefficient in Figure 2, is shown in Figure 4. An interesting feature that can be deduced from Figure 3 is that the reflection at the interface acts as a filter with respect to a broadband signal; this is especially true at high angles of incidence.
Figure 2: Absolute value of the reflection coefficient R as function of the angle of incidence for the driving frequencies 10 Hz, 100 Hz, 1 kHz, and 10 kHz.
Figure 3: Absolute value of the reflection coefficient R as function of frequency for the angles of incidence 30°, 40°, 50°, 60°, 70°, and 80°.
Figure 4: Absorption coefficient α as function of the angle of incidence for the driving frequencies 10 Hz, 100 Hz, 1 kHz, and 10 kHz.
As can be seen from Figure 2, the reflection coefficient has significantly different behavior for 3 of the driving frequencies at an incidence angle of, for example, 72°. The total pressure is shown in Figure 5 and the displacement field is shown in Figure 6. Note the different length scales as the computational domain (geometry) scales with the wavelength.
From the graphs in Figure 2 and Figure 4, it is evident that the behavior shifts for the different frequencies for increasing angles of incidence. At 90°, the reflection coefficient is of course 1 and the absorption 0.
Figure 5: Total pressure distribution for an incidence angle of 72° for 10 Hz (top left), 100 Hz (top right), 1 kHz (bottom left), and 10 kHz (bottom right). Note that the computational domain size (geometry) scales with the wavelength.
Figure 6: Displacement amplitude with deformation of the porous matrix for an incidence angle of 72° for 10 Hz (top left), 100 Hz (top right), 1 kHz (bottom left), and 10 kHz (bottom right). Note that the computational domain size (geometry) scales with the wavelength.
Notes About the COMSOL Implementation
•
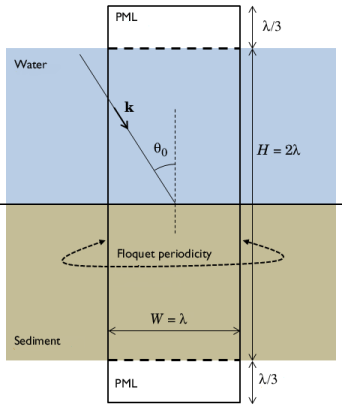
In order for the model to be numerically well behaved for all frequencies studied, the geometry of the periodic unit cell is set to depend on the wavelength lambda0. This means that the geometry depends on the frequency. In COMSOL Multiphysics, it is not permitted to have a frequency-dependent geometry in the Frequency Domain solver. To circumvent this problem, a parametric sweep is added. The sweep parameter is the frequency f0, which is then entered as the study frequency in the Frequency Domain study step.
•
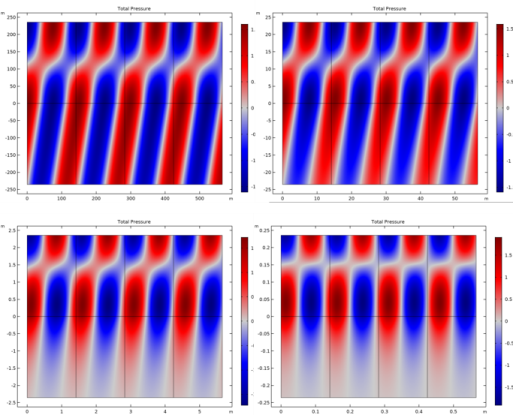
The periodic plots shown in Figure 5 and Figure 6 are set up using a Periodic 2D data set. Using the Floquet-Bloch periodicity option and entering the wave vector components k0x and k0y with this option, the correct phase is automatically added to the underlying solution variables.
•
From the material parameters in Table 1, it is seen that the Biot-Willis coefficient αB is close to 1. This means that the porous matrix is in a so-called limp configuration. At the other extreme, when αB is close to the value of porosity εP, the configuration is named rigid (the skeleton is not moving). When a porous material is in one of these states it is possible to use an equivalent fluid model from the Poroacoustics domain feature (found in the Pressure Acoustics, Frequency Domain interface) to model the porous material. Use, for example, the Johnson-Champoux-Allard (limp frame option) for the case studied here. The advantage of using this model is that it is much less computationally expensive than the full Biot model. An equivalent fluid model generates or mimics the losses in the porous domain and therefore predicts the reflection and absorption coefficient. However, it does not account for the details of the movement of the skeleton and the propagation of the three different types of waves. Moreover, as soon as a porous material is neither limp nor rigid, the full Biot model of the Poroelastic Waves interface is necessary.
Reference
1. R.D. Stoll and T.-K. Kan, “Reflections of Acoustic Waves at a Water-Sediment Interface”, J. Acoust. Soc. Am., vol. 70, no. 1, pp. 149–156, 1981.
Application Library path: Acoustics_Module/Underwater_Acoustics/reflections_water_sediment
Modeling Instructions
Start by adding the Acoustic-Poroelastic Waves Interaction multiphysics interface. The interface consists of the Pressure Acoustics, Frequency Domain interface, the Poroelastic Waves interface, and the necessary Multiphysics coupling.
From the File menu, choose New.
New
In the New window, click Model Wizard.
Model Wizard
1
In the Model Wizard window, click 2D.
2
In the Select Physics tree, select Acoustics>Acoustic-Structure Interaction>Acoustic-Poroelastic Waves Interaction.
3
Click Add.
4
Click Study.
5
In the Select Study tree, select General Studies>Frequency Domain.
6
Click Done.
Geometry 1
First, load the model parameters from a file. The list contains definitions of material parameters (see Table 1), geometry lengths, and the two model parameters (frequency f0 and angle of incidence theta0).
Global Definitions
Parameters 1
1
In the Model Builder window, under Global Definitions click Parameters 1.
2
In the Settings window for Parameters, locate the Parameters section.
3
Click Load from File.
4
Browse to the model’s Application Libraries folder and double-click the file reflections_water_sediment_parameters.txt.
Build the geometry, a sketch is given in Figure 1.
Geometry 1
Rectangle 1 (r1)
1
In the Geometry toolbar, click Rectangle.
2
In the Settings window for Rectangle, locate the Size and Shape section.
3
In the Width text field, type W.
4
In the Height text field, type H.
5
Click to expand the Layers section. Clear the Layers on bottom check box.
6
Select the Layers on top check box.
7
In the table, enter the following settings:
Layer name
Thickness (m)
Layer 1
Hpml
8
Click Build Selected.
Rectangle 2 (r2)
1
In the Geometry toolbar, click Rectangle.
2
In the Settings window for Rectangle, locate the Size and Shape section.
3
In the Width text field, type W.
4
In the Height text field, type H.
5
Locate the Position section. In the y text field, type -H.
6
Locate the Layers section. In the table, enter the following settings:
Layer name
Thickness (m)
Layer 1
Hpml
7
Click Build All Objects.
8
Click the Zoom Extents button in the Graphics toolbar.
Under the Definitions node add variables as well as two coupling operators. The two operators act as probes picking up variable values. One samples a point in the water domain and the other evaluates the average over the water-sediment interface.
Definitions
Variables 1
1
In the Model Builder window, under Component 1 (comp1) right-click Definitions and choose Variables.
2
In the Settings window for Variables, locate the Variables section.
3
Click Load from File.
4
Browse to the model’s Application Libraries folder and double-click the file reflections_water_sediment_variables.txt.
Integration 1 (intop1)
1
In the Definitions toolbar, click Nonlocal Couplings and choose Integration.
2
In the Settings window for Integration, locate the Source Selection section.
3
From the Geometric entity level list, choose Point.
4
Select Point 4 only.
Average 1 (aveop1)
1
In the Definitions toolbar, click Nonlocal Couplings and choose Average.
2
In the Settings window for Average, locate the Source Selection section.
3
From the Geometric entity level list, choose Boundary.
4
Select Boundary 6 only.
Now, create selections to be used when setting up the physics.
Explicit 1
1
In the Definitions toolbar, click Explicit.
2
In the Settings window for Explicit, type Porous Domain in the Label text field.
3
Select Domains 1 and 2 only.
Explicit 2
1
In the Definitions toolbar, click Explicit.
2
In the Settings window for Explicit, type Water Domain in the Label text field.
3
Select Domains 3 and 4 only.
Proceed to set up the physics and boundary conditions of the problem. The condition at the water-sediment interface is defined under the Multiphysics node.
The properties of the porous material are edited after adding the porous material.
Poroelastic Waves (pelw)
1
In the Model Builder window, under Component 1 (comp1) click Poroelastic Waves (pelw).
2
In the Settings window for Poroelastic Waves, locate the Domain Selection section.
3
From the Selection list, choose Porous Domain.
4
Locate the Sound Pressure Level Settings section. From the Reference pressure for the sound pressure level list, choose Use reference pressure for water.
Periodic Condition 1
1
In the Physics toolbar, click Boundaries and choose Periodic Condition.
2
Select Boundaries 1, 3, 10, and 11 only.
3
In the Settings window for Periodic Condition, locate the Periodicity Settings section.
4
From the Type of periodicity list, choose Floquet periodicity.
5
Specify the kF vector as
k0x
X
k0y
Y
Pressure Acoustics, Frequency Domain (acpr)
1
In the Model Builder window, under Component 1 (comp1) click Pressure Acoustics, Frequency Domain (acpr).
2
In the Settings window for Pressure Acoustics, Frequency Domain, locate the Domain Selection section.
3
From the Selection list, choose Water Domain.
4
Locate the Sound Pressure Level Settings section. From the Reference pressure for the sound pressure level list, choose Use reference pressure for water.
Periodic Condition 1
1
In the Physics toolbar, click Boundaries and choose Periodic Condition.
2
Select Boundaries 5, 7, 12, and 13 only.
3
In the Settings window for Periodic Condition, locate the Periodicity Settings section.
4
From the Type of periodicity list, choose Floquet periodicity.
5
Specify the kF vector as
k0x
x
k0y
y
6
In the Model Builder window, click Pressure Acoustics, Frequency Domain (acpr).
7
In the Settings window for Pressure Acoustics, Frequency Domain, locate the Typical Wave Speed for Perfectly Matched Layers section.
8
In the cref text field, type real(acpr.c_c).
Background Pressure Field 1
1
In the Physics toolbar, click Domains and choose Background Pressure Field.
2
In the Settings window for Background Pressure Field, locate the Domain Selection section.
3
From the Selection list, choose Water Domain.
4
Locate the Background Pressure Field section. From the Pressure field type list, choose User defined.
5
In the pb text field, type Pin.
Materials
Material 1 (mat1)
In the Model Builder window, under Component 1 (comp1) right-click Materials and choose Blank Material, twice, to create two new blank materials.
Material 2 (mat2)
1
In the Model Builder window, under Component 1 (comp1)>Materials click Material 2 (mat2).
2
In the Settings window for Material, type Water in the Label text field.
3
In the Settings window for Material, type Sediment in the Label text field.
Now, go to the Poroelastic Material node and specify the porous matrix material parameters to be taken from the Sediment material that you just created. When done, return to the material, where it is now evident which parameters to define.
Poroelastic Waves (pelw)
Poroelastic Material 1
1
In the Model Builder window, under Component 1 (comp1)>Poroelastic Waves (pelw) click Poroelastic Material 1.
2
In the Settings window for Poroelastic Material, locate the Porous Matrix Properties section.
3
From the Porous elastic material list, choose Sediment (mat2).
4
Locate the Fluid Properties section. From the Viscosity model list, choose Biot’s high frequency range.
5
From the Specify list, choose Characteristic pore size.
6
In the a text field, type a.
Materials
Material 1 (mat1)
1
In the Model Builder window, under Component 1 (comp1)>Materials click Material 1 (mat1).
2
In the Settings window for Material, locate the Material Contents section.
3
In the table, enter the following settings:
Property
Variable
Value
Unit
Property group
Density
rho
rhoF
kg/m³
Basic
Speed of sound
c
c0
m/s
Basic
Dynamic viscosity
mu
muF
Pa·s
Basic
Compressibility of fluid
chif
1/Kf
1/Pa
Basic
Sediment (mat2)
1
In the Model Builder window, click Sediment (mat2).
2
In the Settings window for Material, locate the Material Contents section.
3
In the table, enter the following settings:
Property
Variable
Value
Unit
Property group
Bulk modulus
K
Kbc
N/m²
Bulk modulus and shear modulus
Shear modulus
G
Gc
N/m²
Bulk modulus and shear modulus
Density
rho
rhod
kg/m³
Basic
Porosity
epsilon
epsilonP
1
Basic
Permeability
kappa_iso ; kappaii = kappa_iso, kappaij = 0
kappaP
m²
Basic
Biot-Willis coefficient
alphaB
alphaB0
1
Poroelastic material
Tortuosity factor
tau
tau0
1
Poroacoustics model
Multiphysics
Acoustic-Porous Boundary 1 (apb1)
Now is a good time to inspect the Multiphysics node and look at the multiphysics coupling. Click on Acoustic-Porous Boundary 1. You can see that it is active on the interface between the water domain and the porous sediment.
The last step before building the mesh is to set up and define the perfectly matched layers (PMLs). Define one for the poroelastic domain and another for the water domain.
Definitions
Perfectly Matched Layer 1 (pml1)
1
In the Definitions toolbar, click Perfectly Matched Layer.
2
Select Domain 1 only.
3
In the Settings window for Perfectly Matched Layer, locate the Scaling section.
4
From the Coordinate stretching type list, choose Rational.
5
From the Physics list, choose Poroelastic Waves (pelw).
Perfectly Matched Layer 2 (pml2)
1
In the Definitions toolbar, click Perfectly Matched Layer.
2
Select Domain 4 only.
3
In the Settings window for Perfectly Matched Layer, locate the Scaling section.
4
From the Coordinate stretching type list, choose Rational.
Keep the default setting in the Physics list, that is Pressure Acoustics, Frequency Domain (acpr).
Build the mesh by following the instructions below. When modeling systems with interfaces between porous domains and fluid domains the mesh is important; it should be very fine at the interface and it is good practice to use a single boundary layer mesh element in the porous domain. It is also important for the periodic conditions to have the same mesh at source and destination. Ideally, a mesh sensitivity analysis should be made for models of this kind.
Mesh 1
Edge 1
1
In the Model Builder window, under Component 1 (comp1) right-click Mesh 1 and choose More Operations>Edge.
2
Select Boundaries 11 and 12 only.
Size 1
1
Right-click Edge 1 and choose Size.
2
In the Settings window for Size, locate the Element Size section.
3
Click the Custom button.
4
Locate the Element Size Parameters section. Select the Maximum element size check box.
5
In the associated text field, type lam0/15.
Size 2
1
In the Model Builder window, right-click Edge 1 and choose Size.
2
In the Settings window for Size, locate the Geometric Entity Selection section.
3
From the Geometric entity level list, choose Point.
4
Select Point 8 only.
5
Locate the Element Size section. Click the Custom button.
6
Locate the Element Size Parameters section. Select the Maximum element size check box.
7
In the associated text field, type lam0/40.
8
Click Build Selected.
Copy Edge 1
1
In the Model Builder window, right-click Mesh 1 and choose More Operations>Copy Edge.
2
Select Boundaries 11 and 12 only.
3
In the Settings window for Copy Edge, locate the Destination Boundaries section.
4
Select the Activate selection toggle button.
5
Select Boundaries 3 and 5 only.
6
Click Build Selected.
Free Triangular 1
1
Right-click Mesh 1 and choose Free Triangular.
2
In the Settings window for Free Triangular, locate the Domain Selection section.
3
From the Geometric entity level list, choose Domain.
4
Select Domains 2 and 3 only.
Size 1
1
Right-click Free Triangular 1 and choose Size.
2
In the Settings window for Size, locate the Element Size section.
3
Click the Custom button.
4
Locate the Element Size Parameters section. Select the Maximum element size check box.
5
In the associated text field, type lam0/15.
6
Select the Maximum element growth rate check box.
7
In the associated text field, type 1.1.
Size 2
1
In the Model Builder window, right-click Free Triangular 1 and choose Size.
2
In the Settings window for Size, locate the Geometric Entity Selection section.
3
From the Geometric entity level list, choose Boundary.
4
Select Boundary 6 only.
5
Locate the Element Size section. Click the Custom button.
6
Locate the Element Size Parameters section. Select the Maximum element size check box.
7
In the associated text field, type lam0/40.
Size 3
1
Right-click Free Triangular 1 and choose Size.
2
In the Settings window for Size, locate the Geometric Entity Selection section.
3
From the Geometric entity level list, choose Point.
4
Select Points 3 and 8 only.
5
Locate the Element Size section. Click the Custom button.
6
Locate the Element Size Parameters section. Select the Maximum element size check box.
7
In the associated text field, type lam0/40.
8
Click Build Selected.
Mapped 1
In the Model Builder window, right-click Mesh 1 and choose Mapped.
Distribution 1
1
In the Model Builder window, right-click Mapped 1 and choose Distribution.
2
Select Boundaries 1 and 7 only.
3
In the Settings window for Distribution, locate the Distribution section.
4
In the Number of elements text field, type 20.
5
Click Build Selected.
Boundary Layers 1
1
In the Model Builder window, right-click Mesh 1 and choose Boundary Layers.
2
In the Settings window for Boundary Layers, locate the Domain Selection section.
3
From the Geometric entity level list, choose Domain.
4
Select Domain 2 only.
5
Click to expand the Transition section. Clear the Smooth transition to interior mesh check box.
Boundary Layer Properties
1
In the Model Builder window, click Boundary Layer Properties.
2
In the Settings window for Boundary Layer Properties, locate the Boundary Layer Properties section.
3
In the Number of boundary layers text field, type 1.
4
From the Thickness of first layer list, choose Manual.
5
In the Thickness text field, type lam0/400.
6
Select Boundary 6 only.
7
Click Build All.
The finalized mesh should look like that in the figure below.
Study 1
1
In the Model Builder window, click Study 1.
2
In the Settings window for Study, locate the Study Settings section.
3
Clear the Generate default plots check box.
Step 1: Frequency Domain
1
In the Model Builder window, under Study 1 click Step 1: Frequency Domain.
2
In the Settings window for Frequency Domain, locate the Study Settings section.
3
In the Frequencies text field, type f0.
4
Click to expand the Study Extensions section. Select the Auxiliary sweep check box.
5
From the Sweep type list, choose All combinations.
6
Click Add.
7
In the table, enter the following settings:
Parameter name
Parameter value list
Parameter unit
theta0 (Incidence angle)
range(0,pi/2/39,pi/2)
rad
Parametric Sweep
1
In the Study toolbar, click Parametric Sweep.
2
In the Settings window for Parametric Sweep, locate the Study Settings section.
3
Click Add.
4
In the table, enter the following settings:
Parameter name
Parameter value list
Parameter unit
f0 (Driving frequency)
10 100 1000 10000
Hz
5
In the Study toolbar, click Compute.
Results
Add a selection to the data set to only plot results in the physical domains (not in the PMLs). You can study the behavior of the PMLs by removing this selection again or creating a separate data set without the selection.
Datasets
In the Model Builder window, expand the Results node.
Selection
1
In the Model Builder window, expand the Datasets node.
2
Right-click Study 1/Parametric Solutions 1 (sol2) and choose Selection.
3
In the Settings window for Selection, locate the Geometric Entity Selection section.
4
From the Geometric entity level list, choose Domain.
5
Select Domains 2 and 3 only.
Now, also add an array dataset in order to easily plot the result in the periodic structure.
Array 2D 1
1
In the Results toolbar, click More Datasets and choose Array 2D.
2
In the Settings window for Array 2D, locate the Data section.
3
From the Dataset list, choose Study 1/Parametric Solutions 1 (sol2).
4
Locate the Array Size section. In the X size text field, type 4.
5
Click to expand the Advanced section. Select the Floquet-Bloch periodicity check box.
6
Find the Wave vector subsection. In the X text field, type k0x.
7
In the Y text field, type k0y.
Now, create four different 2D plots representing the incident pressure (background pressure), the reflected pressure (scattered pressure), the total pressure, and the displacement in the porous matrix.
2D Plot Group 1
1
In the Results toolbar, click 2D Plot Group.
2
In the Settings window for 2D Plot Group, type Incident Pressure in the Label text field.
3
Click to expand the Title section. From the Title type list, choose Manual.
4
In the Title text area, type Incident Pressure.
5
Clear the Parameter indicator text field.
Surface 1
1
Right-click Incident Pressure and choose Surface.
2
In the Settings window for Surface, locate the Expression section.
3
In the Expression text field, type acpr.p_b.
4
Locate the Coloring and Style section. From the Color table list, choose Wave.
5
Select the Symmetrize color range check box.
Arrow Surface 1
1
In the Model Builder window, right-click Incident Pressure and choose Arrow Surface.
2
In the Settings window for Arrow Surface, locate the Expression section.
3
In the X component text field, type k0x.
4
In the Y component text field, type k0y.
5
Locate the Arrow Positioning section. Find the X grid points subsection. In the Points text field, type 5.
6
Locate the Coloring and Style section. From the Color list, choose Black.
Incident Pressure
1
In the Model Builder window, click Incident Pressure.
2
In the Settings window for 2D Plot Group, locate the Data section.
3
From the Dataset list, choose Study 1/Parametric Solutions 1 (sol2).
4
From the Parameter value (freq (Hz),theta0 (rad)) list, choose 4: freq=10000 Hz, theta0=0.12083 rad.
Select any of the desired combinations of the frequency f0 and the angle of incidence theta0 and plot to have a look at the results. You may need to use the Zoom Extent tool as the geometry depends on the frequency.
5
In the Incident Pressure toolbar, click Plot.
6
Click the Zoom Extents button in the Graphics toolbar.
2D Plot Group 2
1
In the Home toolbar, click Add Plot Group and choose 2D Plot Group.
2
In the Settings window for 2D Plot Group, type Reflected Pressure in the Label text field.
3
Locate the Data section. From the Dataset list, choose Study 1/Parametric Solutions 1 (sol2).
4
From the Parameter value (freq (Hz),theta0 (rad)) list, choose 4: freq=10000 Hz, theta0=0.12083 rad.
5
Locate the Title section. From the Title type list, choose Manual.
6
In the Title text area, type Reflected Pressure.
7
Clear the Parameter indicator text field.
Surface 1
1
Right-click Reflected Pressure and choose Surface.
2
In the Settings window for Surface, locate the Expression section.
3
In the Expression text field, type acpr.p_s.
4
Locate the Coloring and Style section. From the Color table list, choose Wave.
5
Select the Symmetrize color range check box.
6
In the Reflected Pressure toolbar, click Plot.
Surface 2
1
In the Model Builder window, right-click Reflected Pressure and choose Surface.
2
In the Settings window for Surface, locate the Expression section.
3
In the Expression text field, type pelw.p_s.
4
Click to expand the Inherit Style section. From the Plot list, choose Surface 1.
5
In the Reflected Pressure toolbar, click Plot.
Note that this gives the scattered field in the water domain while it is equal to the total acoustic field in the porous domain.
In the next figure, plot the total pressure (air and porous domains). Use the periodic data set to display the periodic nature of the modeled system.
The Floquet-periodic nature of the solution is recovered with the selected Floquet-Bloch periodicity option in the Array 2D data set. With this option the correct phase is added to the underlying solution variables.
2D Plot Group 3
1
In the Home toolbar, click Add Plot Group and choose 2D Plot Group.
2
In the Settings window for 2D Plot Group, type Total Pressure in the Label text field.
3
Locate the Data section. From the Dataset list, choose Array 2D 1.
4
From the Parameter value (freq (Hz),theta0 (rad)) list, choose 4: freq=10000 Hz, theta0=0.12083 rad.
5
Locate the Title section. From the Title type list, choose Manual.
6
In the Title text area, type Total Pressure.
7
Clear the Parameter indicator text field.
Surface 1
1
Right-click Total Pressure and choose Surface.
2
In the Settings window for Surface, locate the Expression section.
3
In the Expression text field, type if(dom==3,acpr.p_t,pelw.p_t).
The if() statement plots acpr.p_t if in the water domain (domain 3) else it plots pelw.p_t (the sediment domain).
4
Locate the Coloring and Style section. From the Color table list, choose Wave.
5
Select the Symmetrize color range check box.
6
In the Total Pressure toolbar, click Plot.
7
Click the Zoom Extents button in the Graphics toolbar.
Now, plot the total displacement of the porous matrix. Again use the periodic data set to represent the periodic nature of the modeled system, just as for the total pressure.
2D Plot Group 4
1
In the Home toolbar, click Add Plot Group and choose 2D Plot Group.
2
In the Settings window for 2D Plot Group, type Displacement in the Label text field.
3
Locate the Title section. From the Title type list, choose Manual.
4
In the Title text area, type Displacement.
5
Clear the Parameter indicator text field.
6
Locate the Data section. From the Dataset list, choose Array 2D 1.
7
From the Parameter value (freq (Hz),theta0 (rad)) list, choose 4: freq=10000 Hz, theta0=0.12083 rad.
Surface 1
1
Right-click Displacement and choose Surface.
2
In the Settings window for Surface, locate the Expression section.
3
In the Expression text field, type pelw.disp.
Deformation 1
1
Right-click Surface 1 and choose Deformation.
2
In the Settings window for Deformation, locate the Expression section.
3
In the x component text field, type u.
4
In the y component text field, type v.
5
Locate the Scale section. Select the Scale factor check box.
6
In the associated text field, type 4e9.
7
In the Displacement toolbar, click Plot.
8
Click the Zoom Extents button in the Graphics toolbar.
The total pressure and the displacement are depicted in Figure 5 and Figure 6 for several combinations of the driving frequency and the angle of incidence.
Create Figure 2 from Ref. 1 by plotting the absolute value of the reflection coefficient as function of the angle of incidence for four values of the frequency f0.
1D Plot Group 5
1
In the Home toolbar, click Add Plot Group and choose 1D Plot Group.
2
In the Settings window for 1D Plot Group, type Reflection Coefficient vs. theta0 in the Label text field.
3
Locate the Data section. From the Dataset list, choose None.
4
Locate the Plot Settings section. Select the x-axis label check box.
5
In the associated text field, type Angle of incidence (deg.).
6
Select the y-axis label check box.
7
In the associated text field, type abs(R).
8
Click to expand the Title section. From the Title type list, choose Manual.
9
In the Title text area, type Reflection Coefficient vs. Angle of Incidence.
10
Locate the Axis section. Select the Manual axis limits check box.
11
In the x minimum text field, type -2.
12
In the x maximum text field, type 92.
13
In the y minimum text field, type 0.
14
Locate the Legend section. From the Position list, choose Upper left.
Global 1
1
Right-click Reflection Coefficient vs. theta0 and choose Global.
2
In the Settings window for Global, locate the Data section.
3
From the Dataset list, choose Study 1/Parametric Solutions 1 (sol2).
4
From the Parameter selection (f0) list, choose From list.
5
In the Parameter values list, select 10.
6
Locate the y-Axis Data section. In the table, enter the following settings:
Expression
Unit
Description
absR
1
Absolute value of the surface-averaged reflection coefficient
7
Locate the x-Axis Data section. From the Parameter list, choose Expression.
8
In the Expression text field, type theta0/pi*180.
9
Click to expand the Legends section. From the Legends list, choose Manual.
10
In the table, enter the following settings:
Legends
f0 = 10 Hz
11
In the Reflection Coefficient vs. theta0 toolbar, click Plot.
Global 2
1
Right-click Global 1 and choose Duplicate.
2
In the Settings window for Global, locate the Data section.
3
In the Parameter values list, select 100.
4
Locate the Legends section. In the table, enter the following settings:
Legends
f0 = 100 Hz
Global 3
1
Right-click Global 2 and choose Duplicate.
2
In the Settings window for Global, locate the Data section.
3
In the Parameter values list, select 1000.
4
Locate the Legends section. In the table, enter the following settings:
Legends
f0 = 1 kHz
Global 4
1
Right-click Global 3 and choose Duplicate.
2
In the Settings window for Global, locate the Data section.
3
In the Parameter values list, select 10000.
4
Locate the Legends section. In the table, enter the following settings:
Legends
f0 = 10 kHz
5
In the Reflection Coefficient vs. theta0 toolbar, click Plot.
The plot should look like the one in Figure 2.
Next, create a second study to sweep over the frequency for a given number of angles of incidence.
Add Study
1
In the Home toolbar, click Add Study to open the Add Study window.
2
Go to the Add Study window.
3
Find the Studies subsection. In the Select Study tree, select General Studies>Frequency Domain.
4
Click Add Study in the window toolbar.
5
In the Home toolbar, click Add Study to close the Add Study window.
Study 2
1
In the Model Builder window, click Study 2.
2
In the Settings window for Study, locate the Study Settings section.
3
Clear the Generate default plots check box.
Step 1: Frequency Domain
1
In the Model Builder window, under Study 2 click Step 1: Frequency Domain.
2
In the Settings window for Frequency Domain, locate the Study Settings section.
3
In the Frequencies text field, type f0.
4
Locate the Study Extensions section. Select the Auxiliary sweep check box.
5
From the Sweep type list, choose All combinations.
6
Click Add.
7
In the table, enter the following settings:
Parameter name
Parameter value list
Parameter unit
theta0 (Incidence angle)
30[deg] 40[deg] 50[deg] 60[deg] 70[deg] 80[deg]
rad
Parametric Sweep
1
In the Study toolbar, click Parametric Sweep.
2
In the Settings window for Parametric Sweep, locate the Study Settings section.
3
Click Add.
4
In the table, enter the following settings:
Parameter name
Parameter value list
Parameter unit
f0 (Driving frequency)
10^{range(1,4/14,5)}
Hz
5
In the Study toolbar, click Compute.
Results
Create Figure 3 from Ref. 1 by plotting the absolute value of the reflection coefficient as function of the frequency f0 for six values of the angle of incidence.
1D Plot Group 6
1
In the Home toolbar, click Add Plot Group and choose 1D Plot Group.
2
In the Settings window for 1D Plot Group, type Reflection Coefficient vs. f0 in the Label text field.
3
Locate the Data section. From the Dataset list, choose None.
4
Locate the Title section. From the Title type list, choose Manual.
5
In the Title text area, type Reflection Coefficent vs. Driving Frequency.
6
Locate the Plot Settings section. Select the x-axis label check box.
7
In the associated text field, type Driving Frequency (Hz).
8
Select the y-axis label check box.
9
In the associated text field, type abs(R).
10
Locate the Axis section. Select the Manual axis limits check box.
11
In the Reflection Coefficient vs. f0 toolbar, click Plot.
12
In the Model Builder window, under Results click Reflection Coefficient vs. f0.
13
In the Settings window for 1D Plot Group, locate the Legend section.
14
From the Position list, choose Lower left.
Global 1
1
Right-click Reflection Coefficient vs. f0 and choose Global.
2
In the Settings window for Global, locate the Data section.
3
From the Dataset list, choose Study 2/Parametric Solutions 2 (sol8).
4
From the Parameter selection (freq, theta0) list, choose Manual.
5
In the Parameter indices (1-6) text field, type 1.
6
Locate the y-Axis Data section. In the table, enter the following settings:
Expression
Unit
Description
absR
1
Absolute value of the surface-averaged reflection coefficient
7
Locate the x-Axis Data section. From the Axis source data list, choose Outer solutions.
8
From the Parameter list, choose Expression.
9
In the Expression text field, type f0.
10
Locate the Legends section. From the Legends list, choose Manual.
11
In the table, enter the following settings:
Legends
theta0 = 30[deg]
Global 2
1
Right-click Global 1 and choose Duplicate.
2
In the Settings window for Global, locate the Data section.
3
In the Parameter indices (1-6) text field, type 2.
4
Locate the Legends section. In the table, enter the following settings:
Legends
theta0 = 40[deg]
Global 3
1
Right-click Global 2 and choose Duplicate.
2
In the Settings window for Global, locate the Data section.
3
In the Parameter indices (1-6) text field, type 3.
4
Locate the Legends section. In the table, enter the following settings:
Legends
theta0 = 50[deg]
Global 4
1
Right-click Global 3 and choose Duplicate.
2
In the Settings window for Global, locate the Data section.
3
In the Parameter indices (1-6) text field, type 4.
4
Locate the Legends section. In the table, enter the following settings:
Legends
theta0 = 60[deg]
Global 5
1
Right-click Global 4 and choose Duplicate.
2
In the Settings window for Global, locate the Data section.
3
In the Parameter indices (1-6) text field, type 5.
4
Locate the Legends section. In the table, enter the following settings:
Legends
theta0 = 70[deg]
Global 6
1
Right-click Global 5 and choose Duplicate.
2
In the Settings window for Global, locate the Data section.
3
In the Parameter indices (1-6) text field, type 6.
4
Locate the Legends section. In the table, enter the following settings:
Legends
theta0 = 80[deg]
5
In the Reflection Coefficient vs. f0 toolbar, click Plot.
The plot should look like the one in Figure 3.
Finally, plot the absorption coefficient as function of the frequency f0 for six values of the angle of incidence. Simply duplicate the plot with the absorption coefficient, change absR to alpha in the plots, and rename titles where necessary.
Reflection Coefficient vs. theta0.1
1
In the Model Builder window, right-click Reflection Coefficient vs. theta0 and choose Duplicate.
2
In the Settings window for 1D Plot Group, type Absorption Coefficient vs. theta0 in the Label text field.
3
Locate the Title section. In the Title text area, type Absorption Coefficient vs. Angle of Incidence.
4
Locate the Plot Settings section. In the y-axis label text field, type alpha.
5
Locate the Legend section. From the Position list, choose Lower left.
Global 1
1
In the Model Builder window, expand the Results>Absorption Coefficient vs. theta0 node, then click Global 1.
2
In the Settings window for Global, locate the y-Axis Data section.
3
In the table, enter the following settings:
Expression
Unit
Description
alpha
1
 
Global 2
1
In the Model Builder window, click Global 2.
2
In the Settings window for Global, locate the y-Axis Data section.
3
In the table, enter the following settings:
Expression
Unit
Description
alpha
1
 
Global 3
1
In the Model Builder window, click Global 3.
2
In the Settings window for Global, locate the y-Axis Data section.
3
In the table, enter the following settings:
Expression
Unit
Description
alpha
1
 
Global 4
1
In the Model Builder window, click Global 4.
2
In the Settings window for Global, locate the y-Axis Data section.
3
In the table, enter the following settings:
Expression
Unit
Description
alpha
1
 
4
In the Absorption Coefficient vs. theta0 toolbar, click Plot.
The plot should look like the one in Figure 4.