
|
|
1
|
|
2
|
|
3
|
Click Add.
|
|
4
|
Click Study.
|
|
5
|
|
6
|
Click Done.
|
|
1
|
|
2
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
Click OK.
|
|
6
|
|
7
|
|
8
|
|
9
|
Click OK.
|
|
10
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
Click OK.
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
Click OK.
|
|
6
|
|
7
|
|
8
|
|
9
|
Click OK.
|
|
1
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
Click OK.
|
|
1
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
In the Add dialog box, in the Selections to add list, choose Optimizing region, BH relationship region, and Other solid parts.
|
|
5
|
Click OK.
|
|
6
|
|
1
|
|
2
|
|
3
|
In the tree, select Built-in>Air.
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
1
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
4
|
Locate the Constitutive Relation B-H section. From the Magnetization model list, choose Remanent flux density.
|
|
5
|
Specify the e vector as
|
|
1
|
|
2
|
|
3
|
|
1
|
In the Model Builder window, under Component 1 (comp1) right-click Mesh 1 and choose More Operations>Edge.
|
|
1
|
|
2
|
|
3
|
Click the Custom button.
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
1
|
|
2
|
In the Settings window for Study, type Original geometry BH curve description in the Label text field.
|
|
3
|
|
1
|
|
2
|
|
3
|
Click Add.
|
|
5
|
|
1
|
|
2
|
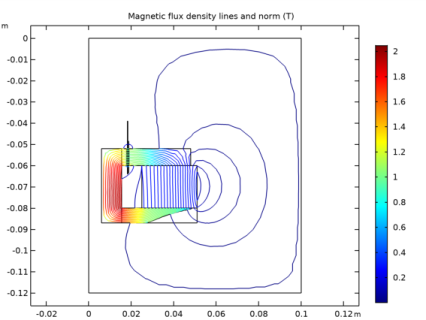
In the Settings window for 2D Plot Group, type Magnetic Flux Density, Direct Model in the Label text field.
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
1
|
|
2
|
In the Settings window for 2D Plot Group, type Magnetic Flux Density, Direct Model (original geometry) in the Label text field.
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
3
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
In the Model Builder window, expand the Original geometry BH curve description>Solver Configurations node, then click Study 2.
|
|
2
|
In the Settings window for Study, type Original geometry nonlinear mur description in the Label text field.
|
|
3
|
|
1
|
|
2
|
|
3
|
Click Add.
|
|
1
|
|
2
|
|
3
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
Locate the Constitutive Relation B-H section. From the μr list, choose User defined. In the associated text field, type murOfB(mf.normB).
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
In the Physics and variables selection tree, select Component 1 (comp1)>Magnetic Fields (mf)>Manual BH relationship.
|
|
5
|
Click Disable.
|
|
1
|
|
2
|
In the Model Builder window, expand the Solution 4 (sol4) node, then click Compile Equations: Stationary.
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
3
|
|
5
|
|
1
|
Go to the Table window.
|
|
3
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
3
|
|
4
|
|
5
|
Locate the Discretization section. From the Shape function type list, choose Discontinuous Lagrange.
|
|
6
|
|
1
|
|
2
|
|
3
|
|
1
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
1
|
|
3
|
|
4
|
|
1
|
In the Model Builder window, under Component 1 (comp1) right-click Definitions and choose Variables.
|
|
2
|
|
3
|
|
5
|
Locate the Variables section. In the table, enter the following settings:
|
|
1
|
In the Model Builder window, under Component 1 (comp1)>Magnetic Fields (mf) click Manual BH relationship.
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
Click Add.
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
In the Model Builder window, expand the Solution 7 (sol7) node, then click Compile Equations: Stationary.
|
|
3
|
|
4
|
|
5
|
In the Model Builder window, expand the Optimization with target 37[cm^3]>Solver Configurations>Solution 7 (sol7)>Optimization Solver 1>Stationary 1 node, then click Fully Coupled 1.
|
|
6
|
|
7
|
|
8
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
Right-click Topology Variable Distribution for Optimization with Target 37[cm^3] and choose Surface.
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
Select the Plot check box.
|
|
4
|
From the Plot group list, choose Topology Variable Distribution for Optimization with Target 37[cm^3].
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
Find the Initial values of variables solved for subsection. From the Settings list, choose User controlled.
|
|
3
|
|
4
|
|
5
|
|
6
|
In the Settings window for Study, type Optimization with target filling=0.5 in the Label text field.
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
Right-click Topology Variable Distribution for Optimization with Target 37[cm^3] and choose Duplicate.
|
|
3
|
|
4
|
|
5
|
In the Label text field, type Topology Variable Distribution for Optimization with Target Filling 50%.
|
|
1
|
|
2
|
|
3
|
Select the Plot check box.
|
|
4
|
From the Plot group list, choose Topology Variable Distribution for Optimization with Target Filling 50%.
|
|
5
|
|
1
|
In the Model Builder window, right-click Magnetic Flux Density, Direct Model (original geometry) and choose Duplicate.
|
|
2
|
In the Settings window for 2D Plot Group, type Magnetic Flux Density Norm for Optimization with Target Filling 50% in the Label text field.
|
|
3
|
Locate the Data section. From the Dataset list, choose Optimization with target filling=0.5/Solution 8 (sol8).
|
|
4
|
|
5
|
|
1
|
In the Model Builder window, under Component 1 (comp1)>Optimization (opt) click Control Variable Field 1.
|
|
2
|
|
3
|
|
4
|
|
1
|
In the Model Builder window, under Component 1 (comp1)>Optimization (opt) click Control Variable Field 1.
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
Click Plot.
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
Click the Export button.
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
In the Filename text field, enter the path to the temporary file just exported, or click Browse and navigate to it.
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
In the Physics and variables selection tree, select Component 1 (comp1)>Magnetic Fields (mf)>Manual BH relationship.
|
|
4
|
Click Disable.
|
|
1
|
|
2
|
|
3
|
Click Add.
|
|
5
|
|
6
|
In the Settings window for Study, type Direct solution built with surface extracted from optimization result in the Label text field.
|
|
7
|
|
1
|
In the Model Builder window, expand the Results>Magnetic Flux Density for Optimization with Target Filling 50% node, then click Surface 1.
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
From the Dataset list, choose Direct solution built with surface extracted from optimization result/Solution 9 (sol9).
|
|
4
|
|
1
|
In the Model Builder window, right-click Direct solution built with surface extracted from optimization result/Parametric Solutions 3 (sol10) and choose Selection.
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
In the Model Builder window, under Results click Magnetic Flux Density Norm, Revolved Geometry (mf).
|
|
2
|
In the Settings window for 3D Plot Group, type Revolved Representation of Magnetic Flux Density for Optimization with Target Filling 50% in the Label text field.
|
|
3
|
|
4
|
In the Revolved Representation of Magnetic Flux Density for Optimization with Target Filling 50% toolbar, click Plot.
|