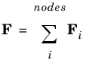Theory for Joint Forces and Moments Computation
The joint forces and moments are evaluated in the global spatial coordinate system as well as in a joint local coordinate system. The joint forces and moments are referred to the center of joint in the current position. For the joints that have translational degrees of freedom, the center of joint should be interpreted as fixed to the source side.
Summing Reaction Forces Over the Boundaries
This is the default method for computing the joint forces and moments when flexible domains are attached to the joint. The computation can be done on either the source or destination attachment. The convention is that the force and moment are the ones acting on the attachment from the joint. The sign changes if you switch between using the source or destination attachment for the evaluation.
The joint forces are computed by integrating (that is, a summation over all nodes) the reaction forces on the attached boundaries.
The joint moments are computed first by integrating the cross product of reaction forces and position vector of each node relative to the centroid of the attached boundaries and then transferring it to the center of the joint.
Here the subscript ‘a’ indicates the centroid of attachment, and ‘c’ indicates the center of joint. Ra is the rotation matrix representing the rotation of the attachment, and u represents the displacements.
Using Weak Constraints
When using weak constraints, the joint constraints are applied in a weak form, and the values of the Lagrange multipliers give the joint forces (Fw) and moments (Mw). This works for both flexible and rigid components. The use of Lagrange multipliers can, however, have an effect on the structure of the equation system, which limits the solvers that can be used.
The joint forces and moments are computed as
The correction term for the moment appears in joints that have translational degrees of freedom because Mw is computed on the destination attachment, which can have moved relative to the source attachment.
The sign convention in this case is that the forces and moments should be interpreted as acting on the destination attachment.
Using Penalty Formulation
When using penalty method, the joint constraints are applied using a penalty formulation, and the values of the penalty forces (Fp) and moments (Mp) give the joint forces and moments. This works for both flexible and rigid components. Moreover, this also works for overconstrained rigid-body systems in which the weak constraints method might not work due to an insufficient number of equations for the Lagrange multipliers.
Since the value of penalty factor directly affects the joint constraints, it should be chosen judiciously. The penalty factor value should be large enough to ensure that the joint constraints are not violated beyond a permissible limit. At the same time the penalty factor should not be too high, since that will make the system of equations numerically ill-conditioned.
The penalty forces (Fp) and moments (Mp) are computed as
where cu and cθ are the translational and rotational violations of the joint constraints, respectively. The penalty factor pj is the input having a default value, 0.1dEequ. In this expression, Eequ is an effective Young’s modulus, and d is the geometric diagonal of the bounding box of the geometry.
The computation of joint forces and moments using penalty forces and moments is as described above for the weak constraints method: