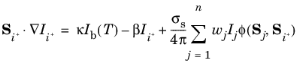Discrete Ordinates Method Implementation in 2D

For a given index i, define two indices, i+ and i−, so that

•

Ω, Si+, and Si- have the same components in the xy–plane

•

and Si+ and Si- have opposite components in the z direction.

Assuming that a model is invariant in the z direction, the radiative transfer equation in two directions, Si+ and Si-, for the discrete ordinates method (DOM) reads:

Halving the sum of the two equations above and using

can be rewritten as a function of Si ⋅ Sj, as it is in the COMSOL Multiphysics implementation, then

and

In addition

so the above equation can be simplified:

(4-98)

with

since the third component of

is zero in 2D.

Also notice that

(4-99)

with

Using results from Equation 4-98 and Equation 4-99 the DOM is formulated in 2D using only radiative intensities,

, on half of the 3D DOM directions,

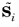
, except for the scattering term. In other expressions than the scattering term, the z component of the radiative intensities Ii and of the discrete directions Ωi can be ignored (or set to zero) and the weight wi, multiplied by 2.