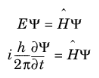Introduction to the Schrödinger Equation

The Schrödinger equation (from the Austrian physicist Erwin Schrödinger) is an equation that describes the behavior of the quantum state of a physical system as it changes in time:

where Ψ is the quantum mechanical wave function (the probability amplitude for different configurations of the system) and

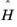
is the Hamiltonian. h, the Planck constant, over 2π is often called the reduced Planck constant (h-bar).

For describing the standing wave solutions of the time-dependent equation, which are the states with definite energy, the equation can be simplified to a stationary Schrödinger equation. The following version of the stationary Schrödinger equation models the atom as a one-particle system:

(4-1)

The equation parameters are:

•

h (approximately 6.626·10−34 Js) is the Planck constant

•

μ is the reduced mass

•

V is the potential energy

•

E is the unknown energy eigenvalue

•

Ψ is the quantum mechanical wave function

The physics interface in this example implements this form of the stationary Schrödinger equation.