All Expression fields supports tensor variables and operators for tensors. If you, for example, want the cross product between two vectors, simply type
directly in the Expression field. The symbol for the cross product is among the standard mathematical symbols defined by the Unicode standard. Other special symbols used by expressions are the (inner) dot product,
A · B, and the nabla operator,
∇A. The system font must support the special symbols to display them properly; otherwise, the expression might not look correct. It is always possible to copy-paste them from an editor that supports Unicode input or directly from a Unicode character map.
|
|
|
|
|
|
|
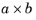 or cross(a,b) or cross(a,b) |
|
|
|
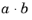 or dot(a,b) or dot(a,b) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
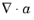 or or divergence(a) |
|
|
|
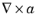 or or curl(a) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
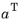 or or transpose(a) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Let r = {x,y,z}
f(r.1..n) becomes f(x,y,z)
g(r.1..2) becomes g(x,y)
|
|
|
|
Let M be a matrix that is symmetric, M = {{u*u, u*v, u*w}, {v*u, v*v, v*w}, {w*u, w*v, w*w}}. Symmetry cannot be detected because v*u is different than u*v by string comparison. The symmetric operator forces symmetry: symmetric(M) = {{u*u, u*v, u*w} , {u*v, v*v, v*w} , {u*w, v*w, w*w}}
|
|
|
|
Let r = {r,phi,z} in 2D axial symmetry
|
|
|
|
Let r = {r,phi,z} in 2D axial symmetry
|
|
|
|
(a+b)*2*pi*r in 2D axial symmetry
(a+b)*ie1.detInvT for an infinite element domain
|
|
|
|
Let T0 be a global parameter set to 300K,
evalConst(1[µm]) becomes 1e-6 if the base unit is meter.
|
|
|
|
Let u be a vector-valued dependent variable with components u, v, and w and the coordinate names x, y, and z. Then
|
The double dot product is a summation over two indices:
Unfortunately, there are two definitions of the double dot product, and the above is referred to the Frobenius inner product or the
colon product. The other definition has flipped order for the indices in the second factor
The gradient operator can be suffixed with
s,
m,
g, or
M to specify in regard to which coordinate variables (spatial, material, geometry, or mesh frame, respectively) it should take its derivatives. Example
∇.m.u is the gradient of the variable
u in the material frame.
The eval operator makes it possible to control the evaluation context locally in an expression. The operator must be preceded by one of the frame prefixes:
M (mesh),
g (geometry),
m (material), and
s (spatial). The
eval operator can, for example, be used in the subnode definition of a variable declaration to provide an automatic transform for all frames but one. Assume that you have a declaration on all frames for a variable named
A. The definition subnode of this declaration has the expression
m.eval(A), which means that the evaluation context is locally changed to the material frame. The evaluation in that frame will always pick up the declaration in the material frame,
[AX, AY, AZ] and then transform it to the frame of the evaluation context of the definition. This results in three definitions for each of the declarations, where the definitions for geometry and spatial will have an automatic transform using the material variable. The definition of the material variable, on the other hand, will have a circular reference to itself. This last definition has to be replaced with a separate
Variable Definition node on the same selection with a explicit definition (for example, a shape definition).
The subst operator,
mat.subst can replace model inputs inside expressions of material properties. The syntax is as follows:
The first argument must be the name of a material property with or without the mat prefix. If the prefix is missing, it will be automatically added to the given name. The model input arguments are either variable names or field names of model inputs (for example,
T or
temperature) with or without the
minput prefix. Again, the prefix will be added if missing. The replacements arguments are parsed as ordinary expressions and must match the tensor size of the model input argument it belongs to.