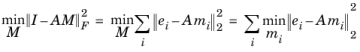The goal of the sparse approximate inverse (Sparse Approximate Inverse (SAI)) preconditioner is to construct a preconditioner matrix M that is an approximate inverse of the system matrix A. The matrix is constructed by solving the minimization problem

This problem is easily parallelizable because the problems are independent for each column mi, but because each problem involves solving the equation A mi =  ei, it is costly to construct the matrix M. In general the resulting matrix M is dense. This problem is circumvented by constructing an approximation to M. The goal of the approximation matrix is that it should be sparse. One way of achieving this goal is to predefine a sparsity pattern for M with an associated index set I. Then the problem is reduced to

where Ii is the index set for column i. Because A is sparse and pi is zero for all entries that are not part of the index set Ii, there is a corresponding index set Ji that defines the row to solve for. Therefore the original problem is reduced to a least-squares problem

for each column pi in P. The index set can be chosen as the one of the system matrix or of a power of the system matrix. Symmetric problems can be treated using the symmetrization (P + PT) /2.