The SOR (successive over-relaxation) method provides a simple and memory-efficient solver/preconditioner/smoother based on classical iteration methods for solving a linear system
A x = b. Given a relaxation factor
ω (usually between
0 and
2), a sweep of the SOR method transforms an initial guess
x0 to an improved approximation
x1 = x0 + M−1(b − Ax0), where the preconditioning matrix
M = L + D/ω, and
D is the diagonal part of
A, and
L is the strictly lower triangular part of
A. When
ω = 1 (the default), the Gauss-Seidel method is obtained.
In the SORU method, M = U + D/ω, where
U is the strictly upper triangular part of
A. The SOR and SORU methods use a more accurate approximation of the matrix, which leads to fewer iterations but slightly more work per iteration than in the Jacobi method.
When the system matrix A is symmetric, the SSOR method has the advantage that the preconditioning matrix
M is symmetric. Symmetry of the preconditioner matrix is necessary when using the conjugate gradients iterative method. In such cases, the SSOR preconditioner is preferable to the SOR preconditioner.
The SOR Gauge algorithms are described.
Magnetostatic problems are often formulated in terms of a magnetic vector potential. The solution of problems formulated with such a potential is in general not unique. Infinitely many vector potentials result in the same magnetic field, which typically is the quantity of interest. A finite element discretization of such a problem results in a singular linear system of equations, Ax = b. Despite being singular, these systems can be solved using iterative solvers if the right-hand side of the discretized problem is the range of the matrix
A. For discretized magnetostatic problems, the range of
A consists of all divergence-free vectors. Even if the right side of the mathematical problem is divergence free, the right side of the finite element discretization might not be numerically divergence free. To ensure that
b is in the range of
A, SOR gauge performs a divergence cleaning of the right side by using the matrices
T and
TT similar to the algorithm for the
SOR Vector iterative method. To this end, the system
TTTψ = −TTb is first solved. Adding
Tψ to
b then makes the numerical divergence of the right side small.
In regions where the mesh is sufficiently anisotropic, the algorithm forms lines of nodes (
SOR Line) that connect nodes that are relatively close to each other (
Ref. 34). Thus, in a boundary layer, a line is a curve along the thin direction of the mesh elements. A smoothing iteration does two things:
The SOR Vector algorithm is an implementation of the concepts in
Ref. 31 and
Ref. 19. The algorithm applies SOR iterations on the main linear equation
Ax =
b but also makes SOR iterations on a projected linear equation
TTAT y = TTb. Here the projection matrix,
T, is the discrete gradient operator, which takes values of a scalar field in the mesh vertices and computes the vector-element representation of its gradient. Loosely speaking, the argument for using this projection is the following: For example, let the linear equation
Ax = b represent the discretization of a PDE problem originating from the vector Helmholtz equation
for the unknown vector field E, where
a and
c are scalars, and
F is some right-hand side vector. Standard preconditioners/smoothers cannot smooth the error in the null space of the operator
∇ × (a∇ × .). This null space is the range of the gradient operator. This algorithm adds a correction
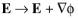
to the standard SOR smoothed solution (or residual), where it computes

from SOR iterations on a projected auxiliary problem. The projected problem is obtained by taking the divergence (or discretely
−TT) of the Helmholtz equation and plugging in the correction. You then obtain
(for clarity, boundary constraints are disregarded), which, if c is definite (strictly positive or strictly negative), is a standard elliptic type of equation for the scalar field
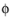
.
The projection matrix T is computed in such a way that nonvector shape functions are disregarded, and you can therefore use it in a multiphysics setting. It can also handle contributions from different geometries. Nonvector shape function variables are not affected by the correction from the projected system, and the effects on them are the same as when you apply the standard SOR algorithm.