For the Fully Coupled attribute, you can define one of the settings for the double dogleg method. Also see Termination Criterion for the Fully Coupled and Segregated Attribute Nodes.

The double dogleg method (Ref. 25) is available for stationary problems. It is a Newton trust region method and can as such adjust the direction as well as the step length when solving the nonlinear equation , : .

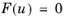
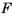
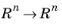
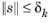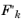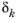
subject to . Here, is the Jacobian of F at the current point uk, Fk = F(uk), and the size of the double dogleg step s is required to be bounded by the current trust region radius . Both the Cauchy point — that is, the minimizer of m in the steepest descent direction — and the Newton point are utilized by the double dogleg method. If the Newton step size is smaller than the trust region radius, the full Newton step is taken. Otherwise, the method considers both the Newton direction and the steepest descent direction and calculates a step with size equal to the current trust region radius. A damped Newton step is calculated, and if the size of this step is smaller than the trust region radius then the double dogleg step is in the Newton direction, else if the size of the Cauchy step is larger than the trust region radius, the double dogleg step is taken in the steepest descent direction. Otherwise, a convex combination of the Cauchy step and the Newton step is calculated such that the resulting double dogleg step size is equal to the trust region radius. In each iteration, the algorithm dynamically adjusts the size of the trust region depending on the predicted decrease of m compared to the actual one. For further details, see Ref. 25. For difficult problems, you can choose to start the computation by a damped Newton step. Enter the damping factor between 0 and 1 in the Initial damping factor field. The algorithm terminates if the norm of the scaled residual is less than the given tolerance, . 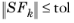You can choose the type of scaling in the Residual scaling list. See the Fully Coupled Method and Termination settings.