The FFT Solver () performs a discrete Fourier transformation for time-dependent or frequency-dependent input solutions using FFT (fast Fourier transform). You can add the FFT solver to Time Dependent and Frequency Domain studies. The FFT solver supports both forward FFT from the time domain to the frequency domain and inverse NFT (nonuniform Fourier transform) or inverse FFT from the frequency domain to the time domain. The input solution has to be of a Time Dependent type for a forward FFT or of a Parametric type for an inverse NFT (INFT) or inverse FFT (IFFT). The input solution can have real-valued or complex-valued data. COMSOL Multiphysics uses the FFT library in Intel’s MKL for the FFT transformations in the FFT solver.

You can visualize the results of an FFT or INFT/IFFT like any other solution, and it can be postprocessed in the same way. The output is typically a complex-valued quantity. Use abs(u) to plot the absolute value, or use real(u) and imag(u) to plot the real and imaginary parts, respectively.

For the forward FFT (the time-dependent case), a time-dependent solution is transformed from times {t0,…, tN−1} to frequencies {f0, …, fN−1} in the frequency domain.

For the inverse NFT or inverse FFT (the frequency domain case), a frequency-dependent solution is transformed from frequencies {f0, …, fN−1} to times {t0, …, tK−1} in the time domain. The FFT algorithm is used for the inverse transformation if the input frequency list and the output time list are equidistant and the output time range given matches the input data. Otherwise, the NFT algorithm is used.

From the Defined by study step list, select a corresponding Frequency to Time FFT or Time to Frequency FFT study step (the default if such a study step created the FFT Solver node; the FFT solver settings are then controlled from the study step), or select User defined to define the corresponding settings in the FFT solver (see below).

From the Transformation list, choose Forward for a forward FFT from the time domain to the frequency domain or Inverse for an inverse NFT/FFT from the frequency domain to the time domain. If a study step controls the FFT solver, the transformation setting is determined from that study step.

From the Prescribed by list, choose Solution (the default) to use a solution as the input to the study, or choose Initial expression to use an expression for the initial values to couple a field to another field. The mapping then occurs before the FFT.

From the Solution list you can select any applicable solution, including solutions from other studies. You can also select Current, which uses the current solution. Depending on the type of solution selected, a Use list may appear where you can choose Automatic, to use the current solution or, if the allowed values are not set correctly, a Solution Store node, or a specified stored solution (Solution Store 1, for example).

For scaling of the solution, from the Scaling list choose Discrete Fourier transform (the default) for discrete scaling (unscaled) or Continuous Fourier transform for continuous scaling (scaled by time or frequency step).

You can apply a window function for the input data by selecting the Use window function check box. A window function can be useful to restrict the input data. The following options are available from the Window function list:

For general information about window functions, see Ref. 20.

In the case of a forward FFT, for all window types except the one defined from a user-defined expression and the cutoff window, you can also specify a time unit (default: s) in the Time unit list provided for the Start time and End time fields or the Window center fields.

In the case of an inverse FFT, for all window types except the one defined from a user-defined expression and the cutoff window, you can also specify a unit (default: Hz) in the Frequency unit list.

From the Input list, choose what type of input to use for the forward FFT:

From the Time unit list, choose a time unit (default: s) to use for the times in the transformation. Specify the input time range ([tstart, tend]) for the forward FFT in the Start time (tstart) and End time (tend) fields. The number of interpolated input solutions, N, is derived from the specified maximum output frequency and appears in the solver log. Specify the maximum output frequency fmax using the Frequency unit list (default: Hz) and the Maximum output frequency field.

The input solution is padded with zeros (for tstart <  t0 and tend >  tN), if the start time or end time for the FFT exceeds the time range [t0,  tN] of the time-dependent input solution. Window functions are applied to the original data (that is, the window function is applied first, then the zero padding is added).

The Periodic input data check box is selected by default. The FFT solver then assumes that u(tend) = u(tstart) and performs the FFT on the values {u(t0),…, u(tN−1)} for the equidistant times t0 = tstart,…, tN−1, where tN = tend; that is, the period T is tend − tstart. The outputs are {ω(f0), …, ω(fN−1)}. The frequencies are computed by fk = k / T for k = 0, …, N−1. If you clear the Periodic input data check box, the FFT solver performs the FFT for the values {u(t0),…, u(tN−1)} for the equidistant times t0 = tstart,…,tN−1 = tend; that is, the period T is (N /( N−1))·(tend − tstart). The outputs are {ω(f0), …, ω(fN−1)}. The frequencies are computed by fk = k / T for k = 0, …, N−1. Note that the period T is different compared to the previous case. The time-dependent input solution is interpolated at the times t0…, tN−1. See the description below for information about how N is determined.

From the Store output frequencies list, choose No negative frequencies for real input (the default) or All frequencies. If you choose No negative frequencies for real input, the number of input samples N is defined by N= 2M + 1, with M = floor((tend−tstart)·fmax). If you choose All frequencies, N is defined by N = M + 1. In the first case, real input data is assumed and instead of ω(f0), …, ω(f2M) only ω(f0),…, ω(fM)) are stored. 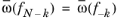This is not a loss of information due to ω(fk) = ω(fk+N) = (a warning is given if the input data is not real).

If you have chosen All frequencies from the Store output frequencies list, then from the Output order list, you can select Natural or Symmetric (the default):

for k = 0, …, N−1.

Solutions in the frequency domain are not interpolated. The input values do not have to be equidistant and they do not have to be sorted with respect to the frequencies. The input data (for nonnegative or nonpositive given frequencies) is by default extended by negative frequencies or positive frequencies with complex-conjugated input values. You can switch this behavior on and off using the Extend input samples list. Choose Add complex conjugate pairs (the default) or Use original data. The first option allows creation of real output data from complex-valued input data by basically recreating data thrown away by the Do not store negative frequencies for real input option for the forward FFT.

From the Frequencies list, select All (the default) or Select from interval:

Choose the time unit from the Time unit list (default: s). Enter the output time range for the inverse NFT/FFT in the Times field. These times correspond to the set of time values selected from the Times to store list. The default is Time steps taken by solver. If you want to use another set of times (perhaps to reduce the size of the output data), select From list and enter the time steps in the Output times field. The output data is then interpolated to these output times. Click the Range button () to define a range of output time values using the Range dialog box. The number of output solutions can be different from the number of input solutions.

The Periodic input data check box is only available if you have selected Use original data from the Extend input samples list. The value for the highest frequency is not considered in the inverse transformation, if the Periodic input data check box is selected.

The inverse FFT is computed for input data ω(f0), …, ω(fN−1) using the following formula:

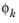
for k = 0, …, N − 1. The correction factor is defined as

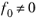
where F = fN− f0, and you can interpret it as a shift of the input values for by means of the following formula:

with ω( fj + N) = ω( fj ) for j = 0, …, N−1.

Performing an unscaled transformation (Scaling list set to Discrete Fourier Transform) means that a forward FFT times an inverse FFT results in the original input data multiplied by a factor of N. The original input is obtained if Scaling is set to Continuous Fourier Transform.

The FFT solver sorts the input data before applying the inverse FFT. For equidistant input frequencies and equidistant output, the fast transformation algorithm (FFT) is applied, if the number of input samples is equal to the number of output time values and if the given output time step (derived from the Output times list) correlates to the input frequency range.

The inverse NFT is computed using the following formula if Use original data is selected from the Extend input samples list:

for k = 0, …, K−1 (K is given by the number of output times; that is, t0, …, tK−1. If you have selected Add complex conjugate pairs from the Extend input samples list, then the formula

for k = 0, …, K−1 is used. The input frequencies f1, …, fM have to be all positive or all negative, and either f0 = 0 is given as input frequency or ω( f0) = 0 is used.

Select the Add stationary solution check box to extend the input data for frequency 0 by a stationary solution that is either taken as the data for frequency 0 or added to the data for frequency 0. Select the method to retrieve the solution from the Method list: Solution (the default) to use the solution itself, or Initial expression to use the expression for the initial value. Choose any available and applicable solution from the Solution list, or choose Zero for no solution. Depending on the selected solution, additional settings appear for specifying which of the solutions to use and which parameter values, eigenfrequencies, or times to use. Use the Time list to select an input solution at a specific time or to interpolate.

You can specify phase functions for input and output data. This functionality can be used for modifying the input and output data. Select the Use phase function check box to specify phase functions. The following options are available from the Phase function for input and Phase function for output lists: None (the default, which provides no phase function) and From expression:

Select From expression to type an expression for the phase function in the Expression field. The expression ein for the input data or eout for the output data can be real-valued or complex-valued. In the forward case, each input value u(tk) is then multiplied by exp(i ein), and similarly, each output value ω(fk) is multiplied by exp(i eout). In the inverse case, each input value ω(fk) is multiplied by exp(i ein), and similarly, each output value u(tk) is multiplied by exp(i eout).

Select the Store intermediate FFT data on disk check box to store intermediate data on disk. The FFT solver then typically becomes slower (due to load and store operations) but uses less memory.

Click the Add button () to add a constant and then define its name in the Constant name column and its value (a numerical value or parameter expression) in the Constant value column. By default, any defined parameters are first added as the constant names, but you can change the names to define other constants. Click Delete () to remove the selected constant from the list.

Select the Keep warnings in stored log check box if you want the warnings to remain in the log for troubleshooting or other use.