The momentum equation (Equation 13-7 or Equation 13-9) is a (nonlinear) convection-diffusion equation. Such equations can easily become unstable if discretized using the Galerkin finite element method. Stabilized finite element methods are usually necessary in order to obtain physical solutions. The stabilization settings are found in the main Fluid Flow interface features. To display this section, click the Show More Options button () and select Stabilization in the Show More Options dialog box.

There are three types of stabilization methods available for Navier-Stokes — streamline diffusion, crosswind diffusion, and isotropic diffusion. Streamline diffusion and crosswind diffusion are consistent stabilization methods, whereas isotropic diffusion is an inconsistent stabilization method.

For optimal functionality, the exact weak formulations of and constants in the streamline diffusion and crosswind diffusion methods depend on the order of the shape functions (basis functions) for the elements. The values of constants in the streamline diffusion and crosswind diffusion methods follow Ref. 5 and Ref. 6.

For strongly coupled systems of equations, the streamline diffusion method must be applied to the system as a whole rather than to each equation separately. These ideas were first explored by Hughes and Mallet (Ref. 8) and were later extended to Galerkin least-squares (GLS) applied to the Navier-Stokes equations (Ref. 9). This is the streamline diffusion formulation that COMSOL Multiphysics supports. The time-scale tensor is the diagonal tensor presented in Ref. 10.

The time-scale tensors for time-dependent problems should in theory depend on a time-scale that many references just set to the time-step taken by the time-solver, Δt (see for example Ref. 9 and Ref. 10). This simple approach doesn’t however necessarily reflect on the actual time-scales in the physics. A typical example is reacting flows where the time-step is often guided by fast reactions, while the flow develops relatively slowly. 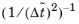COMSOL Multiphysics can therefore replace Δt2 in the time scale tensor with measures of type which are calculated from projections of weak expressions in a fashion similar to those in Ref. 11. These measures of the time scale are used when Use dynamic subgrid timescale check box is selected. Streamline diffusion is active by default because it is necessary when convection is dominating the flow.

Crosswind diffusion can also be formulated for systems of equations, and when applied to the Navier-Stokes equations it becomes a shock-capturing operator. COMSOL Multiphysics supports the formulation in Ref. 9 with a shock-capturing viscosity of the Hughes-Mallet type Ref. 8.