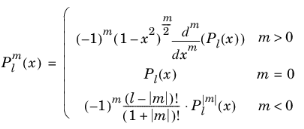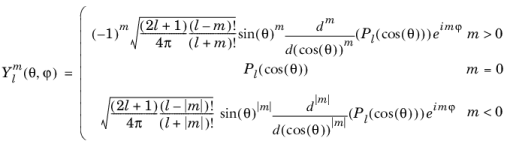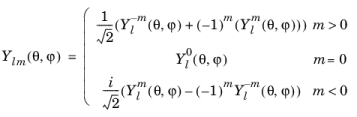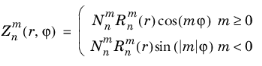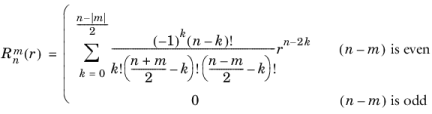These language elements are built-in or user-defined. In addition there are operators that cannot be user-defined, and expressions, which are always user-defined.

Built-in variables have reserved names, names that cannot or should not be redefined by the user. It is not recommended to use a reserved variable name for a user-defined variable, parameter, or function. For some of the most common reserved variable names, such as pi, i, and j, the text where you enter the name turns orange and you get a tooltip message if you select the text string. Reserved function names are reserved only for function names, which means that such names can be used for variable and parameter names, and vice versa. The following tables list most built-in elements and hence those reserved names.

There are three different types of constants: built-in mathematical and numerical constants, built-in physical constants, and parameters. Parameters are user-defined constants that can vary over parameter sweeps. Constants are scalar valued. The following table lists the built-in physical constants. Constants and parameters can have units.

The legendre(l,x) function evaluates a Legendre polynomial Pl(x) of integer degree l:

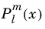
The legendre(l,m,x) function evaluates an associated Legendre polynomial of integer degree l and order m:

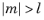
The degree l must be a nonnegative constant integer, and the order m must be a constant integer. For , legendre(l,m,x) returns zero.

The sphericaly(l,m,theta,phi) function evaluates the spherical harmonic function :

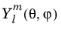
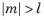
where Pl is the Legendre polynomial of degree l. The degree l must be a nonnegative constant integer, and the order m must be a constant integer. For , sphericaly(l,m,theta,phi) returns zero.

The sphericalyr(l,m,theta,phi) function evaluates the real spherical harmonic function :

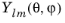
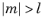
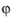
The degree l must be a nonnegative constant integer, and the order m must be a constant integer. For , sphericalyr(l,m,theta,phi) returns zero. The arguments θ and must be real.

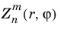
The zernike(m,n,r,phi) function evaluates a Zernike polynomial defined in the following way:

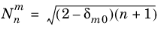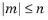
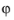
and is the normalization factor. The n argument is required to be a nonnegative constant integer, and the m argument is required to be a constant integer satisfying . The r and arguments are required to be real.

The following table summarizes the built-in variables and constants that are generally available in all COMSOL Multiphysics models. Some are only available in certain geometries or in time-dependent models, for example. These variable names are reserved names and appear in orange in the Settings windows for parameters and variables.

The following user-defined variables generate built-in variables such as space and time derivatives. See Shape Function Variables for information about those built-in variables.