Theory for the Rotating Machinery Interfaces
Both the Rotating Machinery, Laminar Flow and Rotating Machinery, Turbulent Flow interfaces model flow in geometries with rotating parts. For example, stirred tanks, mixers, and pumps.
The Navier-Stokes equations formulated in a rotating coordinate system read (Ref. 1 and Ref. 2)
(4-171)
(4-172)
where v is the velocity vector in the rotating coordinate system, r is the position vector, and Ω is the angular velocity vector. The relation between v and the velocity vector in the stationary coordinate system is
The Rotating Machinery, Fluid Flow interfaces solve Equation 4-171 and Equation 4-172, but reformulated in terms of a nonrotating coordinate system; that is, they solve for u. This is achieved by invoking the Arbitrary Lagrangian-Eulerian Formulation (ALE) machinery. In rotating domains, x = x(Ω, t) as prescribed in the Rotating Domain under Definitions. The Navier-Stokes equations on rotating domains then read
(4-173)
(4-174)
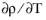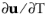
The derivative operator is the mesh time derivative of the density and appears in the equation view as d(rmspf.rho,TIME). Analogously, is the mesh time derivative of the velocity. The variable TIME replaces t as the variable for time.
The user input for a rotating domain prescribes the angular frequency, w. To calculate Ω, the physics interfaces set up an ODE variable for the angular displacement ω. The equation for ω is
(4-175)
Ω, is defined as w times the normalized axis of rotation. In 2D, the axis of rotation is the z direction while it in 3D is specified in the Rotating Domain features. If the model contains several rotating domains, each domain has its own angular displacement ODE variable.
In nonrotating domains, the ordinary Navier-Stokes equations are solved. The rotating and fixed parts need to be coupled together by an identity pair, where a continuity boundary condition is applied.
Wall and Interior Wall boundary conditions apply in the rotating domain provided that the Translational velocity under Wall Movement uses the default Automatic from frame option.
Arbitrary Lagrangian-Eulerian Formulation (ALE) in the COMSOL Multiphysics Reference Manual