Theory for the Viscoelastic Flow Interface
The Viscoelastic Flow Interface is used to simulate incompressible and isothermal flow of viscoelastic fluids. It solves the continuity equation, the momentum balance equation, and a constitutive equation that defines the extra elastic stress contribution. Equation 4-9 and Equation 4-10 become
(4-24)
(4-25)
where the stress tensor is split on a viscous and an elastic contribution as
(4-26)
where μs is the solvent viscosity, S is the strain-rate tensor, and Te is the elastic stress tensor. To adequately describe a flow of fluid with a complex rheological behavior, symmetric stress tensor Te is represented as a sum of the individual modes
(4-27)
To close the equation system, the constitutive relation for each mode is required. Several commonly used constitutive models can be written as a hyperbolic partial differential transport equation of the forms
(4-28)
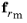
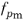
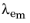
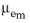
where the relaxation function and the viscosity factor are model specific functions of stress, is a relaxation time, is a polymer viscosity, and the upper convective derivative operator is defined as
(4-29)
The first two terms on the left-hand side of Equation 4-29 represent the material derivative, and the other two terms represent the deformation. For more information, see Ref. 7
Oldroyd-B MODEL
For the Oldroyd B model, the relaxation function and the viscosity factor are given by
(4-30)
The Oldroyd-B model can be derived form the kinetic theory representing the polymer molecules as a suspensions of the Hookean spring in a Newtonian solvent. While demonstrating some basic features of viscoelasticity, the model can only predict a constant shear viscosity and gives unrealistic results for purely extensional flows due to the lack of a mechanism that limits the extensibility.
FENE-P model
The finitely extensible nonlinear elastic model (FENE) is based on the kinetic theory that describes the polymer chains as a non-linear elastic springs and account for finite extension of the polymers monoculars. The FENE model with Peterlin closure (FENE-P) shows a finite extensibility and a shear-thinning behavior. The expressions for the relaxation function and the viscosity factor are given by
(4-31)
where is the extensibility.
Giesekus Model
The Giesekus model is often used to model the flow of the semi-diluted and concentrated polymers. It adds the quadratic nonlinearity that is attributed to the effect of the hydrodynamic drag induced by the polymer-polymer interactions. The corresponding relaxation function and the viscosity factor are given by
(4-32)
where 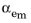is the dimensionless mobility factor.