The model equations that are solved in the Phase Transport Mixture Model interfaces are based on the mass conservation of each phase and on conservation of momentum. The mass conservation equation for each (immiscible) phase
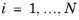
is given by:
where ρi denotes the density (SI unit: kg/m
3),
si denotes the volume fraction (dimensionless), and
ui denotes the velocity vector (SI unit: m/s) of phase
i. In addition, the term
Qi denotes a mass source for phase
i (SI unit: kg/(m
3·s)). It is assumed that the sum of the volume fractions of the phases equals 1:
This means that N − 1 phase volume fractions are independent and are possible to solve for using
Equation 7-83. The volume constraint
Equation 7-84 is used to reduce the number of dependent variables: one volume fraction, let us say of phase
ic (to be specified in the main node of the coupled
Phase Transport interface), is expressed using the other volume fractions:
In the Mixture Model multiphysics coupling feature, it is assumed that the phase
ic is the continuous phase.
In the Phase Transport Mixture Model interfaces it is assumed that the densities of all phases are constant, and therefore the following form of the continuity equation for the mixture can be used
Here ρ is the mixture density (SI unit: kg/m
3) given by:
and τGm is the sum of the viscous and turbulent stresses (SI unit: kg/(m·s
2)).
This relative velocity uri is assumed to be given by two terms
where the slip velocity uslip,i (SI unit: m/s) in the first term is given by one of the slip velocity models discussed below, and where the second term accounts for the turbulent effects, with
Dmd (SI unit: m
2/s) a turbulent dispersion coefficient given by
where σT is the turbulent particle Schmidt number (dimensionless). The particle Schmidt number is usually suggested a value ranging from 0.35 to 0.7.
From this equation, and using the volume constraint Equation 7-84, the velocity of the continuous phase
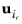
can be written in terms of the mixture velocity
j and the slip velocities
uslip,i as follows: