Note that Equation 7-3, and Equation 7-4 are solved in the contained interface, Laminar Flow or Turbulent Flow interface. Note that the form of the continuity equation, appropriate for high density difference mixtures, differs from the definition in Theory for the Single-Phase Flow Interfaces.

where γ is the reinitialization parameter (set to 1 by default), and ε is the interface thickness controlling parameter (set to hmax/2 where hmax is the maximum element size in the component). The density is a function of the level set function defined as

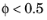
where ρ1 and ρ2 are the constant densities of Fluid 1 and Fluid 2, respectively, and μ1 and μ2 are the dynamic viscosities of Fluid 1 and Fluid 2, respectively. Here, Fluid 1 corresponds to the domain where , and Fluid 2 corresponds to the domain where . 

Further details of the theory for the level set method are in Ref. 1.

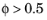
where the quantity λ (SI unit: N) is the mixing energy density and ε (SI unit: m) is a capillary width that scales with the thickness of the interface. These two parameters are related to the surface tension coefficient, σ (SI unit: N/m), through the equation

and γ is the mobility parameter which is related to ε through γ = χε2 where χ is the mobility tuning parameter (set to 1 by default). The volume fraction of Fluid 2 is computed as

where the min and max operators are used so that the volume fraction has a lower limit of 0 and an upper limit of 1. The density is then defined as

where ρ1 and ρ2 are the densities and μ1 and μ2 are the dynamic viscosities of Fluid 1 and Fluid 2, respectively.

where G is the chemical potential defined as:

Details of the theory for the phase field method are found in Ref. 2.

The four forces on the right-hand side of Equation 7-3 are due to gravity, surface tension, a force due to an external contribution to the free energy (using the phase field method only), and a user-defined volume force.

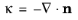
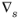
where σ is the surface tensions coefficient (SI unit: N/m), n is the unit normal to the interface, and is the curvature. δ (SI unit: 1/m) is a Dirac delta function located at the interface. is the surface gradient operator

The δ-function is approximated by a smooth function according to

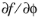
where G is the chemical potential (SI unit: J/m3) defined in The Equations for the Phase Field Method and is a user-defined source of free energy. If Include surface tension gradient effects in surface tension force is selected, extra terms are added to account for the Marangoni effect due to gradients in the surface tension coefficient (see Ref. 6):

The gravity force is Fg = ρg where g is the gravity vector. Add this as a Gravity feature to the fluid domain.