You are viewing the documentation for an older COMSOL version. The latest version is
available here.
The Transport of Concentrated Species (tcs) interface (

), found under the
Chemical Species Transport branch (

) when adding a physics interface, is used to study gaseous and liquid mixtures where the species concentrations are of the same order of magnitude and none of the species can be identified as a solvent. In this case, properties of the mixture depend on the composition, and the molecular and ionic interactions between all species need to be considered. The physics interface includes models for multicomponent diffusion, where the diffusive driving force of each species depends on the mixture composition, temperature, and pressure.
When this physics interface is added, the following default nodes are also added in the Model Builder —
Transport Properties,
No Flux, and
Initial Values. Then, from the
Physics toolbar, add other nodes that implement, for example, boundary conditions and reactions. You can also right-click
Transport of Concentrated Species to select physics features from the context menu.
The Label is the default physics interface name.
The Name is used primarily as a scope prefix for variables defined by the physics interface. Refer to such physics interface variables in expressions using the pattern
<name>.<variable_name>. In order to distinguish between variables belonging to different physics interfaces, the
name string must be unique. Only letters, numbers, and underscores (_) are permitted in the
Name field. The first character must be a letter.
The default Name (for the first physics interface in the model) is
tcs.
(6-1)
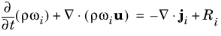
(6-2)
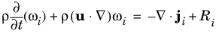
|
•
|
The Maxwell-Stefan option employs the most detailed diffusion model, but is also the most computationally expensive. The model is intended for diffusion dominated models, and requires that the multicomponent Maxwell-Stefan diffusivities of all component pairs are known. No stabilization is available when selecting this model.
|
|
•
|
The Mixture-averaged option is less computationally expensive than the Maxwell-Stefan model. It is a simpler model that can be used when variations in the partial pressures and temperature can be assumed to not affect the multicomponent diffusion. The model includes stabilization but requires the multicomponent Maxwell-Stefan diffusivities of all component pairs.
|
|
•
|
The Fick’s law model is a general model that should be used when the diffusion is assumed Fickian, or when no multicomponent diffusivities are available. Also, when molecular diffusion is not the dominating transport mechanism and a robust but low order model is wanted, the Fick’s law options should be used. The model includes stabilization.
|
Under Additional transport mechanisms, click to select or clear any combination of check boxes as needed.
Select the Migration in electric field check box to activate migration of ionic species due to an electric field. The resulting migration term is part of the relative mass flux vector.
The Mass transport in porous media check box activates functionality specific to species transport in porous media. When selected the following features are enabled:
For Mixture-averaged and
Fick’s law, it is possible to include
Knudsen diffusion. This mechanism accounts for species collisions with the surrounding media, for example, the pore walls the species pass through. It is also an important component when setting up a Dusty gas model.
When using the Maxwell-Stefan diffusion model the relative mass flux vector is
where 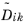 (SI unit: m2
(SI unit: m2/s) are the multicomponent Fick diffusivities,
dk (SI unit: 1/m) is the diffusional driving force,
T (SI unit: K) is the temperature, and
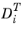
(SI unit: kg/(m·s)) is the thermal diffusion coefficient.
(6-3)
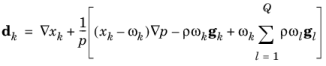
where gk is an external force (per unit mass) acting on species
k. In the case of an ionic species, the external force due to the electric field, which is added by selecting the
Migration in electric field check box, is
(6-4)
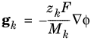
where zk is the species charge number,
F (SI unit: A·s/mol) is Faraday’s constant and
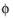
(SI unit: V) is the electric potential.
When using the Mixture-averaged diffusion model, the diffusive flux is formulated in terms of a mixture-averaged diffusion coefficient representing the diffusion of each species into the resulting mixture. The diffusion coefficient is based on the multicomponent Maxwell-Stefan diffusivities
Dik. The
Mixture-averaged diffusion model is computationally less expensive, and significantly more robust than the
Maxwell-Stefan Diffusion Model, but constitutes an approximation of the multicomponent flux. For information on the flux formulation in this case see
Multicomponent Diffusion: Mixture-Averaged Approximation.
When using the Fick’s law diffusion model, the diffusive flux is formulated in terms of a Fickian diffusion coefficient. The
Fick’s law diffusion model is computationally less expensive and significantly more robust than the
Maxwell-Stefan Diffusion Model, but constitutes an approximation of the multicomponent flux. For information on the flux formulation in this case see
Multispecies Diffusion: Fick’s Law Approximation.
Select the species that this physics interface solves for using the mass constraint in Equation 6-37 (that is, its value comes from the fact that the sum of all mass fractions must equal
1). In the
From mass constraint list, select the preferred species. To minimize the impact of any numerical and model introduced errors, use the species with the highest concentration. By default, the first species is used.
(6-5)
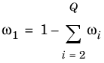
To display this section, click the Show button (

) and select
Stabilization.
The Residual setting applies to both the consistent stabilization methods.
Approximate residual is the default setting and it means that derivatives of the diffusion tensor components are neglected. This setting is usually accurate enough and computationally faster. If required, select
Full residual instead.
To display this section, click the Show button (

) and select
Advanced Physics Options. Normally these settings do not need to be changed.
From the Regularization list, select
On (the default) or
Off. When turned
On, regularized mass fractions are calculated such that
The Diffusion settings are available for the approximate diffusion models Mixture-averaged and Fick’s law.
When the Mixture diffusion correction is enabled, a flux correction is added to ensure that the net diffusive flux is zero. This typically also mean that the solution becomes less sensitive to the species selected to be computed from the mass constraint in the
Species section. More information on this correction is available in the theory section
Multicomponent Diffusion: Mixture-Averaged Approximation.
The Diffusion flux type list controls the whether the molecular flux is assumed proportional to the mole fraction or the mass fraction. See
Multicomponent Diffusion: Mixture-Averaged Approximation or
Multispecies Diffusion: Fick’s Law Approximation for information on the diffusive flux formulation.
The Use pseudo time stepping for stationary equation form option adds pseudo time derivatives to the equation when the
Stationary equation form is used in order to speed up convergence. When selected, a CFL number expression should also be defined. For the default
Automatic option, the local CFL number (from the Courant–Friedrichs–Lewy condition) is determined by a PID regulator. For more information, see
Pseudo Time Stepping for Mass Transport.
|
|
In the COMSOL Multiphysics Reference Manual see Table 2-4 for links to common sections and Table 2-5 to common feature nodes. You can also search for information: press F1 to open the Help window or Ctrl+F1 to open the Documentation window.
|
Specify the Number of species. There must be at least two species. To add a single species, click the
Add concentration button (

) under the table. To remove a species, select it in the list and click the
Remove concentration button (

) under the table. Edit the names of the species directly in the table.