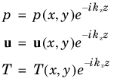The Mode Analysis study type is available for The Thermoviscous Acoustics, Frequency Domain Interface in 2D and 1D axisymmetric models. This type of study is used to determine the form of the
propagating acoustic modes in
waveguide structures. The analyzed 2D and 1D axisymmetric geometries can be thought of as the cross sections of a waveguide. This study is really restricted to the cross section of the waveguides. To calculate the modes in 3D structures at the inlet of the waveguide use
The Thermoviscous Acoustics, Boundary Mode Interface, described below.
The spatial dependency in the (out-of-plane) axial z direction along the waveguide is assumed to be of the form of a traveling wave with wave number
kz. The dependent variables in 2D are rewritten as
Using this form of the dependent variables, differentiation with respect to z reduces to a multiplication with
−ikz. The
propagating modes are determined by solving an eigenvalue problem in the variable
λ = −ikz.
where x is the in plane coordinate(s). The axial wave number is split into a real and an imaginary part. The imaginary part
α of the wave number describes how fast the propagating modes decay along the waveguide, it is often referred to as the attenuation coefficient. The real part
β is related to the phase speed
cph of the propagating mode by
cph =
β/
ω. In thermoviscous acoustics, the obtained wave numbers always have an imaginary part as the modeled system always includes losses. The relation between the angular frequency
ω and the axial wave number
kz is called the dispersion relation.